��Ŀ����
����Ŀ����ֱ֪��y=kx+3��1-k��������kΪ������k��0����kȡ��ͬ��ֵʱ���ɵò�ֱͬ�ߣ���̽����Щֱ�ߵĹ�ͬ������
ʵ������
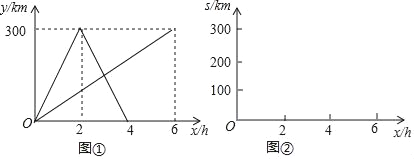
��1����k=1ʱ��ֱ��l1�Ľ���ʽΪ ������ͼ1�л���ͼ��k=2ʱ��ֱ��l2�Ľ���ʽΪ ������ͼ2�л���ͼ��
̽������
��2��ֱ��y=kx+3��1-k���ؾ����㣨 �� ����
���Ǩ��
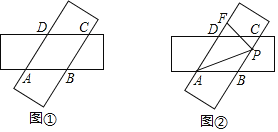
��3������ABCD��ͼ2��ʾ����ֱ��y=kx+k-2��k��0���־���ABCD�����Ϊ��ȵ������֣�����ͼ��ֱ�ӻ�������ֱ�ߣ�
���𰸡���1��y=x����������y=2x-3������������2����3��3������3��������.
��������
��1���ѵ�k=1��k=2ʱ���ֱ������һ�κ����Ľ���ʽ���ɣ�
��2������k��x-3��=y-3���ɵ�����kȡ��ֵ��0���⣩��ֱ��y=kx+3��1-k���ؾ����㣨3��3����
��3�������ֱ��y=kx+k-2��k��0������kȡ��ֵ���ܹ��㣨-1��-2������ȷ�����ζԽ��ߵĽ��㼴�ɻ���ֱ�ߣ�
��1����k=1ʱ��ֱ��l1�Ľ���ʽΪ��y=x��
��k=2ʱ��ֱ��l2�Ľ���ʽΪy=2x-3��
��ͼ1��

��2����y=kx+3��1-k����
��k��x-3��=y-3��
������kȡ��ֵ��0���⣩��ֱ��y=kx+3��1-k���ؾ����㣨3��3����
��3����ͼ2��
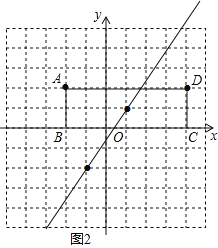
��ֱ��y=kx+k-2��k��0��
��k��x+1��=y+2��
�ࣨk��0������kȡ��ֵ���ܹ��㣨-1��-2����
�ҳ��Խ��ߵĽ��㣨1��1����ͨ�������ֱ��ƽ�־���ABCD�������