题目内容
现有九张背面一模一样的扑克牌，正面分别为：红桃A、红桃2、红桃3、红桃4、黑桃A、黑桃2、黑桃3、黑桃4、黑桃5．
（1）现将这九张扑克牌混合均匀后背面朝上放置，若从中摸出一张，求正面写有数字3的概率是多少？
（2）现将这九张扑克牌分成红桃和黑桃两部分后背面朝上放置，并将红桃正面数字记作m，黑桃正面数字记作n，若从黑桃和红桃中各任意摸一张，求关于x的方程mx2+3x+
=0有实根的概率．（用列表法或画树形图法解，A代表数字1）
（1）现将这九张扑克牌混合均匀后背面朝上放置，若从中摸出一张，求正面写有数字3的概率是多少？
（2）现将这九张扑克牌分成红桃和黑桃两部分后背面朝上放置，并将红桃正面数字记作m，黑桃正面数字记作n，若从黑桃和红桃中各任意摸一张，求关于x的方程mx2+3x+
=0有实根的概率．（用列表法或画树形图法解，A代表数字1）(1)
；(2)
.
；(2).试题分析：（1）九张扑克中数字为3的有2张，即可确定出所求概率；
（2）列表得出所有等可能的情况数，找出方程mx2+3x+
=0有实根的情况数，即可求出所求概率．试题解析：（1）由题意得：九张扑克中数字为3的有2张，即P=
；（2）列表得：
| | 红1 | 红2 | 红3 | 红4 |
| 黑1 | （1，1） | （2，1） | （3，1） | （4，1） |
| 黑2 | （1，2） | （2，2） | （3，2） | （4，2） |
| 黑3 | （1，3） | （2，3） | （3，3） | （4，3） |
| 黑4 | （1，4） | （2，4） | （3，4） | （4，4） |
| 黑5 | （1，5） | （2，5） | （3，5） | （4，5） |
=0有实根，即△=9-mn≥0，即mn≤9的情况有14种，则P=
．考点:1.列表法与树状图法；2.根的判别式；3.概率公式．
练习册系列答案
春雨教育同步作文系列答案
相关题目
．
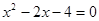的一根，则
．
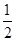)－1－cos45°＋3×(2012－π)0 ⑵解方程：2x2－4x＋1=0 (配方法) 
．
的图象与
轴两个交点的横坐标均为整数，且k为整数，求k的值．
＋
＝________．
,
是关于
的一元二次方程
的两个实数根，且
.
的值.