题目内容
【题目】思维探索:
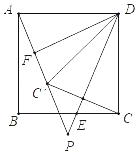
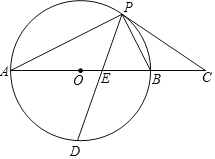
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
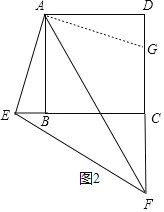
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
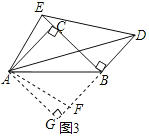
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.

【答案】思维探索:(1)8;(2)12;拓展提升:CE=![]() ﹣1.
﹣1.
【解析】
思维探索:(1)利用旋转的性质,证明△AGE≌△AFE即可;
(2)把△ABE绕点A逆时针旋转90°到AD,交CD于点G,证明△AEF≌△AGF即可求得EF=DF﹣BE;
拓展提升:如图3,过A作AG⊥BD交BD的延长线于G,推出四边形ACBG是矩形,得到矩形ACBG是正方形,根据正方形的性质得到AC=AG,∠CAG=90°,在BG上截取GF=CE,根据全等三角形的性质得到AE=AF,∠EAC=∠FAG,∠ADF=∠ADE=30°,解直角三角形得到DE=DF=4,BE=2![]() ,设CE=x,则GF=CE=x,BC=BG=2
,设CE=x,则GF=CE=x,BC=BG=2![]() ﹣x,根据线段的和差即可得到结论.
﹣x,根据线段的和差即可得到结论.
思维探索:
(1)如图1,将△ADF绕点A顺时针旋转90°得到△ABG,
∴GB=DF,AF=AG,∠BAG=∠DAF,
∵四边形ABCD为正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠BAG+∠BAE=45°=∠EAF,
在△AGE和△AFE中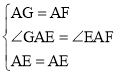
∴△AGE≌△AFE(SAS),
∴GE=EF,
∵GE=GB+BE=BE+DF,
∴EF=BE+DF,
∴△CEF的周长=CE+CF+EF=CE+BE+DF+CF=BC+CD=8,
故答案为:8;
(2)如,2,把△ABE绕点A逆时针旋转90°到AD,交CD于点G,
同(1)可证得△AEF≌△AGF,
∴EF=GF,且DG=BE,
∴EF=DF﹣DG=DF﹣BE,
∴△CEF的周长=CE+CF+EF=CE+CF+DF﹣BE=BC+DF+CF=4+4+2+2=12;
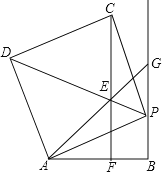
拓展提升:如图3,过A作AG⊥BD交BD的延长线于G,
∵BD⊥BC,∠ACB=90°,
∴∠ACB=∠CBG=∠G=90°,
∴四边形ACBG是矩形,
∵AC=BC,
∴矩形ACBG是正方形,
∴AC=AG,∠CAG=90°,
在BG上截取GF=CE,
∴△AEC≌△AGF(SAS),
∴AE=AF,∠EAC=∠FAG,
∵∠EAD=∠BAC=∠GAB=45°,
∴∠DAF=∠DAE=45°,
∵AD=AD,
∴△ADE≌△ADF(SAS),
∴∠ADF=∠ADE=30°,
∴∠BDE=60°,
∵∠DBE=90°,BD=2,
∴DE=DF=4,BE=2![]() ,
,
设CE=x,则GF=CE=x,BC=BG=2![]() ﹣x,
﹣x,
∴DG=2+2![]() ﹣x,
﹣x,
∴DG﹣FG=DF,
即2+2![]() ﹣x﹣x=4,
﹣x﹣x=4,
∴x=![]() ﹣1,
﹣1,
∴CE=![]() ﹣1.
﹣1.

【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让学生进行摸球试验,每次摸出一个球(放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
|
(1)![]() = ,根据上表数据估计从袋中摸出一个黑球的概率是 .
= ,根据上表数据估计从袋中摸出一个黑球的概率是 .
(2)估算袋中白球的个数为 .
(3)在(2)的条件下,若小强同学从袋中摸出两个球,用画树状图或列表的方法计算摸出的两个球都是白球的概率.