题目内容
【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )
A. 3B. 4C. 5D. 6
【答案】C
【解析】
首先根据勾股定理的逆定理判定△ABC是直角三角形,再根据等腰三角形的性质分别利用AC、BC为腰以及AB为底得出符合题意的图形即可.
解:如图所示:BC=3,AC=4,AB=5,
∵32+42=52,
∴△ABC是直角三角形,∠BAC=90°.
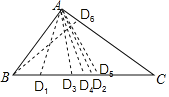
当CD1=AC=4,CD3=AD3,BA=BD4=3,AB=AD2=3,D5A=D5B,BD6=CD6∵△ABC是直角三角形,
∴D3,D5重合,
故能得到符合题意的等腰三角形5个.
故选:C.

练习册系列答案
相关题目