题目内容
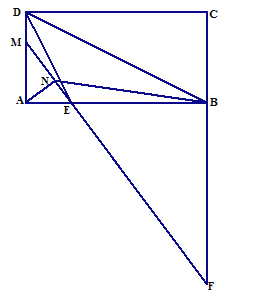
【题目】在矩形 ABCD 中，AB＝3，BC＝4，E、F 是对角线 AC 上的两个动点，分 别从 A、C 同时出发相向而行，速度均为每秒 1 个单位长度，运动时间为 t 秒，其中 0 t 5 ．
（1）若 G，H 分别是 AB，DC 中点，求证：四边形 EGFH 是平行四边形（E、F 相遇时除外）；
（2）在（1）条件下，若四边形 EGFH 为矩形，求 t 的值；
（3）若 G，H 分别是折线 A－B－C，C－D－A 上的动点，与 E，F 相同的速度同时出发，若 四边形 EGFH 为菱形，求 t 的值．
【答案】（1）见解析；（2）0.5或4.5；（3）
【解析】
（1）根据勾股定理求出AC，证明△AFG≌△CEH，根据全等三角形的性质得到GF=HE，同理得到GE=HF，根据平行四边形的判定定理证明；
（2）分AE=CF、AE=CF两种情况，根据矩形的性质计算即可；
（3）连接AG、CH，判定四边形AGCH是菱形，得到AG=CG，根据勾股定理求出BG，得到AB+BG的长，根据题意解答．
（1）证明：∵四边形ABCD是矩形，
∴AB=CD，AB∥CD，AD∥BC，∠B=90°，
∴AC=
，∠GAF=∠HCE，
∵G，H分别是AB，DC中点，
∴AG=BG，CH=DH，
∴AG=CH，
∵AE=CF，
∴AF=CE，
在△AFG和△CEH中，
，
∴△AFG≌△CEH（SAS），
∴GF=HE，
同理：GE=HF，
∴四边形EGFH是平行四边形；
（2）解：由（1）得：BG=CH，BG∥CH，
∴四边形BCHG是平行四边形，
∴GH=BC=4，当EF=GH=4时，平行四边形EGFH是矩形，
分两种情况：①AE=CF=t，EF=5-2t=4，
解得：t=0.5；
②AE=CF=t，EF=5-2（5-t）=4，
解得：t=4.5；
综上所述：当t为0.5s或4.5s时，四边形EGFH为矩形；
（3）解：连接AG、CH，如图所示：
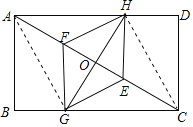
∵四边形EGFH为菱形，
∴GH⊥EF，OG=OH，OE=OF，
∴OA=OC，AG=AH，
∴四边形AGCH是菱形，
∴AG=CG，
设AG=CG=x，则BG=4-x，
由勾股定理得：AB2+BG2=AG2，
即32+（4-x）2=x2，
解得，x=
，
∴BG=
=
，
∴AB+BG=3+=，
∴t为时，四边形EGFH为菱形．
