题目内容
【题目】如图,平面直角坐标系中,已知点A(0,10),点B(m,10)在第一象限,连接AB、OB.
(1)如图1,若OB=12,求m的值.

(2)如图2,当m=10时,过B作BC⊥x轴于C,E为AB边上一点,AE=![]() ,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.
,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.

(3)如图3,将△AOB沿直线OB翻折得到△GOB(点A的对应点为点G),若点G到x轴的距离不大于8,直接写出m的取值范围为 .

【答案】(1)m=![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ≤m≤30
≤m≤30
【解析】
(1)根据勾股定理计算AB的长,可得m的值;
(2)过点F作FM⊥AB,延长MF交OC于点N,由折叠性质可知:EF=AE=![]() ,OF=OA=10,∠EFO=∠OAE=90°,然后根据正方形的性质和AA定理证得△EFM∽△FON,设FM=x,根据相似三角形的性质求得
,OF=OA=10,∠EFO=∠OAE=90°,然后根据正方形的性质和AA定理证得△EFM∽△FON,设FM=x,根据相似三角形的性质求得![]() ,然后利用勾股定理列方程求解x的值,从而求得MF=2,NF=8,ON=6,NC=4,然后再利用勾股定理求得
,然后利用勾股定理列方程求解x的值,从而求得MF=2,NF=8,ON=6,NC=4,然后再利用勾股定理求得![]() 、
、![]() ,
,![]() ,从而利用勾股定理逆定理判定△BCF是直角三角形,从而求解;
,从而利用勾股定理逆定理判定△BCF是直角三角形,从而求解;
(3)由条件可知点G的纵坐标大于或等于-8小于或等于8.分别计算点G的纵坐标为8和-8时m的值可得m的取值范围.
解:(1)由A(0,10),点B(m,10)可知AB⊥y轴,
∵OB=12,OA=10,
∴在Rt△AOB中,AB=![]() ,
,
∴m=![]() ;
;
(2)过点F作FM⊥AB,延长MF交OC于点N
由折叠性质可知:EF=AE=![]() ,OF=OA=10,∠EFO=∠OAE=90°
,OF=OA=10,∠EFO=∠OAE=90°
由题意可知,当m=10时,四边形AOCB是正方形且MN⊥AB
∴MN⊥OC
∴∠EMF=∠FNO=90°
又∵∠EFM+∠OFN=90°,∠OFN+∠FON=90°
∴∠EFM=∠FON
∴△EFM∽△FON
设FM=x,则FN=10-x
∴![]() ,即
,即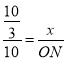 ,解得:
,解得:![]()
∴在Rt△FON中,![]()
解得:x=0(舍去)或x=2
∴MF=2,NF=8,ON=6,NC=4
在Rt△EFM中,![]()
∴![]()
在Rt△MFB中,![]()
在Rt△FNC中,![]()
又∵BC=10=100
∴BF+CF=BC
∴△BCF是直角三角形
即BF⊥CF
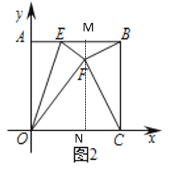
(3)由条件可知点G的纵坐标大于或等于-8小于或等于8.
①当点G的纵坐标为8时,如图,过点G作GK⊥x轴于K,交直线AB于R,
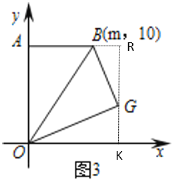
在Rt△OGK中,OG=OA=10,GK=8,可求OK=AR=6,RG=2,
∵BA=BG=m,BR=6-m,
在Rt△BRG中,由![]() ,
,
解得:m=![]() ;
;
②当点G的纵坐标为-8时,如图,过点G作GE⊥x轴于E,交直线AB于R,
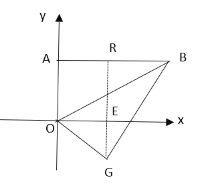
在Rt△OGE中,OG=OA=10,GE=8,
∴OE=AR=6,RE=OA=10,
∴GR=EG+RE=18,
∵∠BGR+∠OGE=∠OGE+∠EOG=90°,
∴∠BGR=∠EOG,
∵∠BRG=∠OEG=90°,
∴△BRG∽△EOG,
∴![]() ,即
,即![]() ,
,
解得:BR=24,
∴BA=m=AR+BR=6+24=30,
综上所述:当![]() ≤m≤30时,点G到x轴的距离不大于8.
≤m≤30时,点G到x轴的距离不大于8.
故答案为:![]() ≤m≤30.
≤m≤30.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案