题目内容
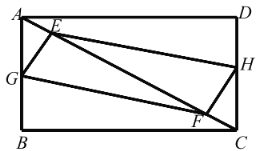
【题目】如图,四边形ABCD为矩形,连接BD,AB=2AD,点E在AB边上,连接ED.
(1)若∠ADE=30°,DE=6,求△BDE的面积;
(2)延长CB至点F使得BF=2AD,连接FE并延长交AD于点M,过点A作AN⊥EM于点N,连接BN,求证:FN=AN+![]() BN.
BN.

【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)在Rt△ADE中,解直角三角形求出EA,DA的值,然后根据AB=2AD求出AB的长,进而求出BE的长,利用三角形的面积公式即可求出面积;
(2)作辅助线,构建全等三角形,证明△FHB≌△ANB,得BH=BN,HF=AN,则△HBN是等腰直角三角形,有NH=![]() NB,根据线段的和代入得结论.
NB,根据线段的和代入得结论.
试题解析:
解:(1)在Rt△ADE中,
∵∠EDA=30°,∴EA= ![]() ED=
ED= ![]() ×6=3,
×6=3,
DA=EDcos30°=6×![]() =3
=3![]() ,
,
∴BE=2DA﹣EA=6![]() ﹣3,∴S△BED=
﹣3,∴S△BED= ![]() ×BE×DA=
×BE×DA= ![]() (6
(6![]() ﹣3)×3
﹣3)×3![]() =
= ![]() ;
;
(2)如图,过B作BH⊥BN,交FM于H,
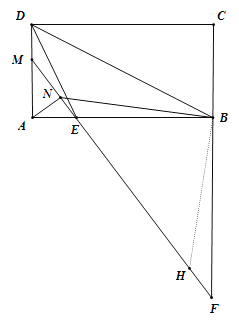
∴∠NBH=∠NBA+∠EBH=90°,
又∵∠ABF=∠HBF+∠EBH=90°,
∴∠NBA=∠HBF,
∵CF∥AD,
∴∠AMN=∠F,
∵AN⊥EM,
∴∠AMN+∠MAN=90°,
∠MAN+∠NAB=90°,
∴∠NAB=∠AMN,
∴∠NAB=∠F,
又∵BF=2AD,AB=2AD,
∴AB=BF,
∴△ANB≌△FHB,
∴BN=BH,AN=FH,
∴△BNH是等腰直角三角形,
∴NH=![]() NB,
NB,
∵FN=FH+NH
=AN+![]() NB/span>.
NB/span>.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目