题目内容
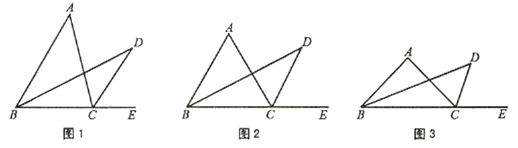
【题目】问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D=;
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D=;这两个图中,与∠A度数的比是 ;
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
【答案】(1)、30°;50°;1:2;(2)、成立;证明过程见解析
【解析】
试题分析:(1)、根据三角形内角和定理以及角平分线的性质分别求出∠D的度数,从而得出∠A和∠D的比值;(2)、根据平分线得出∠ABD=∠DBC,∠ACD=∠DCE,根据外角的性质得出∠ACE=∠ABC+∠A,∠DCE=∠DBC+∠D,从而得出答案.
试题解析:(1)、30;50;1:2;
(2)、成立.∵BD平分∠ABC,∴∠ABD=∠DBC,∵CD平分∠ACE,∴∠ACD=∠DCE,
∵∠ACE是△ABC的外角,∴∠ACE=∠ABC+∠A, 即2∠DCE =2∠DBC+∠A,
∵∠DCE是△BCD的外角,∴∠DCE=∠DBC+∠D,∵2∠DBC+∠A=2(∠DBC+∠D),
∴∠D=![]() ∠A,即∠D:∠A=1:2
∠A,即∠D:∠A=1:2

练习册系列答案
相关题目