题目内容
【题目】如图，已知直线y=ax+b与双曲线y=（x＞0）交于A（x1，y1），B（x2，y2）两点（A与B不重合），直线AB与x轴交于P（x0，0），与y轴交于点C．
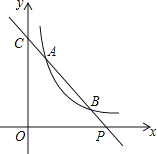
（1）若A，B两点坐标分别为（1，3），（3，y2），求点P的坐标．
（2）若b=y1+1，点P的坐标为（6，0），且AB=BP，求A，B两点的坐标．
（3）结合（1），（2）中的结果，猜想并用等式表示x1，x2，x0之间的关系（不要求证明）．
【答案】（1）P（4，O）；（2）A（2，2），B（4，1）．（3）x1+x2=x0．
【解析】
试题分析：（1）先把A（1，3）），B（3，y2）代入y=
求得反比例函数的解析式，进而求得B的坐标，然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式，继而即可求得P的坐标；
（2）作AD⊥y轴于D，AE⊥x轴于E，BF⊥x轴于F，BG⊥y轴于G，AE、BG交于H，则AD∥BG∥x轴，AE∥BF∥y轴，得出
，
，根据题意得出
，
，从而求得B（
，
y1），然后根据k=xy得出x1 
y1=y1，求得x1=2，代入，解得y1=2，即可求得A、B的坐标；
（3）结合（1），（2）中的结果，猜想x1+x2=x0．
试题解析：（1）∵直线y=ax+b与双曲线y=（x＞0）交于A（1，3），
∴k=1×3=3，
∴y=
，
∵B（3，y2）在反比例函数的图象上，
∴y2=
=1，
∴B（3，1），
∵直线y=ax+b经过A、B两点，
∴
解得
，
∴直线为y=-x+4，
令y=0，则x=4，
∴P（4，O）；
（2）如图，作AD⊥y轴于D，AE⊥x轴于E，BF⊥x轴于F，BG⊥y轴于G，AE、BG交于H，
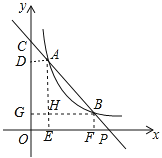
则AD∥BG∥x轴，AE∥BF∥y轴，
∴，，
∵b=y1+1，AB=BP，
∴，，
∴B（，y1）
∵A，B两点都是反比例函数图象上的点，
∴x1y1= y1，
解得x1=2，
代入，解得y1=2，
∴A（2，2），B（4，1）．
（3）根据（1），（2）中的结果，猜想：x1，x2，x0之间的关系为x1+x2=x0．
