��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������y=x2+5x+4�Ķ���ΪM����x�ύ��A��B���㣬��y�ύ��C�㡣
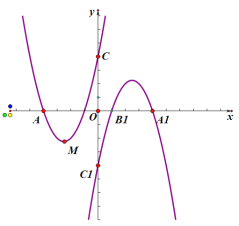
��1�����A��B��C�����ꣻ
��2����������y=x2+5x+4��������ԭ��O�ԳƵ������ߵĺ�������ʽ��
��3���裨2�������������ߵĶ���ΪM1,��x�ύ��A1��B1���㣬��y�ύ��C1�㣬����A��B��C��M��A1��B1��C1��M1��˸����е��ĸ���Ϊ�����ƽ���ı����У�������һ���������ε�ƽ���ı��ε������
���𰸡���1��A��-4��0����B��-1��0����C��0��4������2��y=-x2+5x-4����3��18.
��������
�����������1����y=0�����x��ֵ����x=0�����y�����ɽ��
��2�������A��B��C��������ԭ��O�Գƺ�ĵ�Ϊ��4��0������1��0������0��-4�����ٴ������ʽ�����ɽ��
��3��ȡ�ĵ�A��M��A����M��������AM��MA����A��M����M��A��MM���������ĶԳ��Կ�֪��MM������O��OA=OA����OM=OM�����ɴ��ж��ı���AMA��M��Ϊƽ���ı��Σ���֪AA����MM������ֱ���Ӷ�ƽ���ı���AMA��M���������Σ�����M��MD��x���ڵ�D����������ߵĶ�������M������Sƽ���ı���AMA��M��=2S��AMA�������ɽ��
�����������1����y=0����x2+5x+4=0��
��x1=-4��x2=-1��
��x=0����y=4��
��A��-4��0����B��-1��0����C��0��4����
��2����A��B��C��������ԭ��O�Գƺ�ĵ�Ϊ��4��0������1��0������0��-4����
�����������ߵĺ�������ʽΪy=ax2+bx-4��
����4��0������1��0��������ʽ����![]()
��ã�![]() ��
��
��y=-x2+5x-4��
��3����ͼ��ȡ�ĵ�A��M��A����M��������AM��MA����A��M����M��A��MM����
�����ĶԳ��Կ�֪��MM������O��OA=OA����OM=OM����
���ı���AMA��M��Ϊƽ���ı��Σ�
��֪AA����MM������ֱ��
��ƽ���ı���AMA��M���������Σ�
����M��MD��x���ڵ�D��
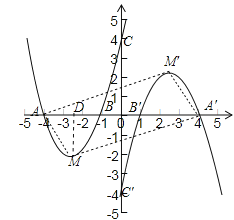
��y=x2+5x+4=(x+![]() )2-
)2-![]() ��
��
��M��-![]() ��-
��-![]() ����
����
����A��-4��0����A����4��0��
��AA��=8��MD=![]() ��
��
��Sƽ���ı���AMA��M��=2S��AMA��=2��![]() ��8��
��8��![]() =18
=18