题目内容
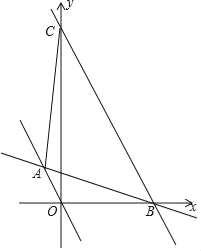
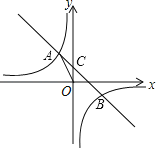
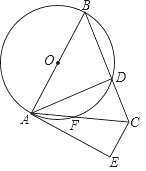
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=10,AC=4![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)AE的长为8.
【解析】
(1)利用平行线的性质,圆的性质和等腰三角形的性质,证明△AEC和△ADC全等即可证明AD=AE,
(2)设AE=AD=x,CE=CD=y,利用勾股定理列出关于x和y的等式,即可求出AE的长.
(1)证明:∵AE与⊙O相切,AB是⊙O的直径,
∴∠BAE=90°,∠ADB=90°,
∵CE∥AB,
∴∠E=90°,
∴∠E=∠ADB,
∵在△ABC中,AB=BC,
∴∠BAC=∠BCA,
∵∠BAC+∠EAC=90°,∠ACE+∠EAC=90°,
∴∠BAC=∠ACE,
∴∠BCA=∠ACE,
又∵AC=AC,
∴△ADC≌△AEC(AAS),
∴AD=AE;
(2)解:设AE=AD=x,CE=CD=y,
则BD=(10﹣y),
∵△AEC和△ADB为直角三角形,
∴AE2+CE2=AC2,AD2+BD2=AB2,
AB=10,AC=4![]() ,AE=AD=x,CE=CD=y,BD=(10﹣y)代入,
,AE=AD=x,CE=CD=y,BD=(10﹣y)代入,
解得:x=8,
即AE的长为8.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】为了响应全民阅读的号召,某社区开展了为期一年的“读书伴我行”阅读活动,在阅读活动开展之初,随机抽取若干名社区居民,对其年阅读量(单位:本)进行了调查统计与分析,结果如下:
平均数 | 中位数 | 众数 | 最大值 | 最小值 | 方差 |
6.9 | 7.5 | 8 | 16 | 1 | 18.69 |
经过一年的“读书伴我行”阅读活动,某社区再次对这部分居民的年阅读量进行调查,并对收集的数据进行了整理、描述和分析,下面给出了部分信息.
a.居民的年阅读量统计表如下:
阅读量 | 2 | 4 | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 16 | 21 |
人数 | 5 | 5 | 5 | 3 | 2 | m | 5 | 5 | 3 | 7 | n |
b.分组整理后的居民阅读量统计表、统计图如下:
组别 | 阅读量/本 | 频数 |
|
| 15 |
|
| |
|
| 13 |
|
|
c.居民阅读量的平均数、中位数、众数、最大值、最小值、方差如下:
平均数 | 中位数 | 众数 | 最大值 | 最小值 | 方差 |
10.4 | 10.5 | q | 21 | 2 | 30.83 |
根据以上信息,回答下列问题:
(1)样本容量为______;
(2)![]() _____;
_____;![]() _____;
_____;![]() ______;
______;
(3)根据社区开展“读书伴我行”阅读活动前、后随机抽取的部分居民阅读量的两组调查结果,请至少从两个方面对社区开展阅读活动的效果进行评价.