题目内容
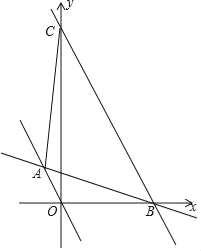
【题目】如图,一次函数y=![]() 的图象与正比例函数y=mx(m≠0)的图象交于点A(a,2),与x轴交于点B.现将直线OA向右平移使其经过点B,平移后的直线与y轴交于点C,连接AC,则四边形AOBC的面积为_____.
的图象与正比例函数y=mx(m≠0)的图象交于点A(a,2),与x轴交于点B.现将直线OA向右平移使其经过点B,平移后的直线与y轴交于点C,连接AC,则四边形AOBC的面积为_____.
【答案】12
【解析】
把点A(a,2)代入y=![]() 得到a=﹣1,把A(﹣1,2)代入y=mx得到m=﹣2,即直线OA解析式为y=﹣2x,再求出B(3,0),设BC的解析式为y=﹣2x+b',把B(3,0)代入求得直线BC的解析式y=﹣2x+6,可得C(0,6),然后根据三角形的面积公式计算即可.
得到a=﹣1,把A(﹣1,2)代入y=mx得到m=﹣2,即直线OA解析式为y=﹣2x,再求出B(3,0),设BC的解析式为y=﹣2x+b',把B(3,0)代入求得直线BC的解析式y=﹣2x+6,可得C(0,6),然后根据三角形的面积公式计算即可.
解:把点A(a,2)代入y=![]() 得,a=﹣1,
得,a=﹣1,
∴A(﹣1,2),
把A(﹣1,2)代入y=mx得,m=﹣2,
∴直线OA解析式为:y=﹣2x,
令y=![]() =0,
=0,
解得:x=3,
∴B(3,0),
由平移可得,BC∥AO,
设BC的解析式为y=﹣2x+b',把B(3,0)代入,可得b'=6,
∴直线BC的解析式为:y=﹣2x+6,
令x=0,则y=6,即C(0,6),
∴OC=6,
∴四边形AOBC的面积=S△ACO+S△BCO=![]() ×6×1+
×6×1+![]() ×6×3=12.
×6×3=12.
故答案为:12.

【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
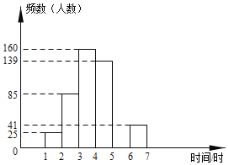
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?