题目内容
【题目】为了响应全民阅读的号召,某社区开展了为期一年的“读书伴我行”阅读活动,在阅读活动开展之初,随机抽取若干名社区居民,对其年阅读量(单位:本)进行了调查统计与分析,结果如下:
平均数 | 中位数 | 众数 | 最大值 | 最小值 | 方差 |
6.9 | 7.5 | 8 | 16 | 1 | 18.69 |
经过一年的“读书伴我行”阅读活动,某社区再次对这部分居民的年阅读量进行调查,并对收集的数据进行了整理、描述和分析,下面给出了部分信息.
a.居民的年阅读量统计表如下:
阅读量 | 2 | 4 | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 16 | 21 |
人数 | 5 | 5 | 5 | 3 | 2 | m | 5 | 5 | 3 | 7 | n |
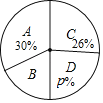
b.分组整理后的居民阅读量统计表、统计图如下:
组别 | 阅读量/本 | 频数 |
|
| 15 |
|
| |
|
| 13 |
|
|
c.居民阅读量的平均数、中位数、众数、最大值、最小值、方差如下:
平均数 | 中位数 | 众数 | 最大值 | 最小值 | 方差 |
10.4 | 10.5 | q | 21 | 2 | 30.83 |
根据以上信息,回答下列问题:
(1)样本容量为______;
(2)![]() _____;
_____;![]() _____;
_____;![]() ______;
______;
(3)根据社区开展“读书伴我行”阅读活动前、后随机抽取的部分居民阅读量的两组调查结果,请至少从两个方面对社区开展阅读活动的效果进行评价.
【答案】(1)50;(2)5、24、16;(3)见解析.
【解析】
(1)由![]() 组人数及其所占百分比可得样本容量;
组人数及其所占百分比可得样本容量;
(2)先根据50个数据的中位数得出![]() 的值,再根据总人数为50,结合表格中的数据及
的值,再根据总人数为50,结合表格中的数据及![]() 的值可得
的值可得![]() ,利用众数的定义可得
,利用众数的定义可得![]() ;
;
(3)从平均数和方差的角度解答(答案不唯一).
(1)样本容量为![]() ,
,
故答案为:50;
(2)∵这50个数据的中位数是第25、26个数据的平均数,且中位数为10.5,
∴![]() ,
,
则![]() 的人数
的人数![]() ,
,
∴![]() ,即
,即![]() ,
,![]() ,
,
故答案为:5、24、16;
(3)从平均数看,“读书伴我行”阅读活动后总体阅读数量有了明显增加;
从方差看,“读书伴我行”阅读活动后阅读数量两级分化扩大(答案不唯一).

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目