题目内容
(本小题6分) 如图,MN为半圆O的直径,半径OA⊥MN, D为OA的中点,过点D作BC//MN,

求证:( 1 ) 四边形ABOC为菱形; (2)∠MNB= ∠BAC
∠BAC

求证:( 1 ) 四边形ABOC为菱形; (2)∠MNB=
 ∠BAC
∠BAC见解析
试题分析:证明:(1)∵BC//MN,半径OA⊥MN
∴BC⊥半径OA
又∵D为OA的中点
∴BC垂直平分OA
∴BA=OB=OA=OC=CA
∴四边形ABOC为菱形——4分
(2)∵BC//MN
∴∠BNM=∠CBN
又∵OB=ON
∴∠BNM=∠NBO
∴∠BNM=
 ∠OBD
∠OBD由(1)知:△ABO和△AOC为正三角形且BD平分∠ABO
∴∠BNM=
 ∠OBD=15°,∠BAC=120°
∠OBD=15°,∠BAC=120°∠MNB=
 ∠BAC ——4分
∠BAC ——4分点评:此类试题属于难度很大的试题,此类试题糅合了菱形等四边形的基本性质定理和判定定理。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
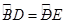 ,连接AD,求证:△ABD≌△ACD.
,连接AD,求证:△ABD≌△ACD.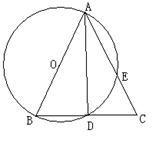
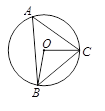

 、
、 的长度分别为
的长度分别为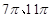 ,则
,则 的长度 .
的长度 .
