题目内容
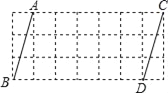
【题目】如图，在每个小正方形的边长均为1的方格纸中有线段AB和CD，点A，B，C，D均在小正方形顶点上．
（1）在方格纸中画出面积为5的等腰直角△ABE，且点E在小正方形的顶点上；
（2）在方格纸中画出面积为3的等腰△CDF，其中CD为一腰，且点F在小正方形的顶点上；
（3）在（1）（2）条件下，连接EF，请直接写出线段EF长．
【答案】（1）见解析（2）见解析（3）
【解析】
（1）以AB为一边，以A为顶点画直角，再确定E的位置，使AB=AE，且面积为5；
（2）画底为2高为3的等腰三角形即可；
（3）利用勾股定理计算出EF的长即可．
（1）如图所示：
根据勾股定理得：AB=AE=
,BE=
∴
，∴△ABE是等腰直角三角形，且面积=
（2）如图所示：
根据勾股定理得：DF =DC=, ∴△DCF是等腰三角形，且面积=
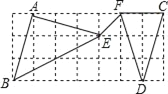
（3）根据勾股定理得：EF＝
＝．
练习册系列答案
相关题目
