题目内容
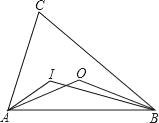
【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。
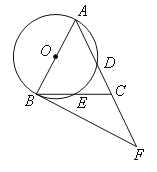
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长。
的长。
【答案】解:(1)如图,连接AE,
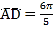
∵AB是⊙O的直径,
∴∠AEB=900,即AE⊥BC。
又∵AB=AC,∴BE=CE。
(2)∵∠BAC=540,AB=AC,∴∠ABC=630。
又∵BF是⊙O的切线,∴∠ABF=900。
∴∠CBF=∠ABF一∠ABC=270。
(3)连接OD,

∵OA=OD,∠BAC=540,∴∠AOD=720。
又∵AB=6,∴OA=2。
∴![]() 。
。
【解析】(1)连接AE,则根据直径所对圆周角是直角的性质得AE⊥BC,从而根据等腰三角形三线合一的性质得出结论。
(2)由∠BAC=540,AB=AC,根据等腰三角形等边对等角的性质和三角形内角和等于零180度求得∠ABC=630;由切线垂直于过切点直径的性质得∠ABF=900,从而由∠CBF=∠ABF一∠ABC得出结论。
(3)连接OD,根据同弧所对圆周角是圆心角一半的性质,求得∠AOD=720,根据弧长公式即可求。

【题目】为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积(平方米) | 单价(万元/平方米) |
不超过30(平方米) | 0.3 |
超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.