Question

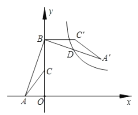
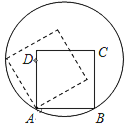
【题目】如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上，顶点C、D在圆内，将正方形ABCD沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时，点C运动的路径长为_____．

Answer 1

【答案】

【解析】

作辅助线，首先求出∠D′AB的大小，进而求出旋转的角度，利用弧长公式问题即可解决．

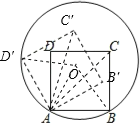
解：如图，分别连接OA、OB、OD′、OC、OC′；

∵OA＝OB＝AB，

∴△OAB是等边三角形，

∴∠OAB＝60°；

同理可证：∠OAD′＝60°，

∴∠D′AB＝120°；

∵∠D′AB′＝90°，

∴∠BAB′＝120°﹣90°＝30°，

由旋转变换的性质可知∠C′AC＝∠B′AB＝30°；

∵四边形ABCD为正方形，且边长为2，

∴∠ABC＝90°，AC＝，

∴当点D第一次落在圆上时，点C运动的路线长为：．

以D或B为圆心滚动时，每次C点运动，

以A做圆心滚动两次，以B和D做圆心滚动三次，

所以总路径＝．

故答案为：π.