题目内容
【题目】二次函数![]() 的图象经过点A(﹣1,4),B(1,0),
的图象经过点A(﹣1,4),B(1,0),![]() 经过点B,且与二次函数
经过点B,且与二次函数![]() 交于点D.
交于点D.
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在BD上方),过N作NP⊥x轴,垂足为点P,交BD于点M,求MN的最大值.
【答案】(1)![]() ;(2)MN的最大值为
;(2)MN的最大值为![]()
【解析】试题分析:(1)根据待定系数法求得即可;
(2)根据待定系数法求得b,得到直线的解析式,设M(m, -![]() ),则N(m,-m2-2m+3),则MN=-m2-2m+3-(-m+)=-m2-2m+3-(-
),则N(m,-m2-2m+3),则MN=-m2-2m+3-(-m+)=-m2-2m+3-(-![]() )=-m2-
)=-m2-![]() =
=![]() 从而求得最大值.
从而求得最大值.
试题解析:(1)∵二次函数![]() 图象经过点A(﹣1,4),B(1,0)
图象经过点A(﹣1,4),B(1,0)
∴![]()
∴m=-2,n=3
∴二次函数的表达式为![]()
(2)![]() 经过点B
经过点B
∴![]()
画出图形
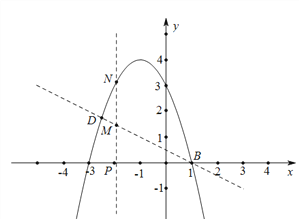
设![]() ,则
,则![]()
所以设MN=![]() =
=![]() =
=![]()
∴MN的最大值为![]()

练习册系列答案
相关题目