Question

【题目】在△ABC中，D、E分别是边AB、BC上的点，AE和CD交于点F，且∠CFE＝∠B。

（1）如图1，求证：∠AEC＝∠CDB；

（2）如图2，过点C作CG⊥AC，交AB于点G，CD⊥CB，∠ACD ＝∠CAB－∠B，求证：AC＝GC；

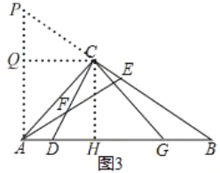
（3）如图3，在（2）的条件下，CE＋CD＝AE，CG＝，求线段BC的长。

Answer 1

【答案】（1）见解析（2）见解析（3）2.

【解析】

（1）在△CEF中，∠ECF+∠CFE+∠CEF=180°，进而得到∠ECF+∠B+∠CEF=180°，在△BCD中，∠BCD+∠B+∠CDB=180°，即可得到结论；

（2）先判断出∠ACD=∠BCG,再根据∠AGC=∠B+∠BCG，即可得到结论；

（3）先判断出四边形AHCQ是正方形，得到CH=CQ,再判断出△CQP≌△CHD，得到∠CPQ=∠CDH，CP=CD,进而得到PE=AE,即∠P=∠PAE,根据（1）的结论，∠AEC＝∠CDB得到∠AEC=∠P=∠PAE,即∠P=60°，再求出∠B=90°-∠P=30°，根据含30°的直角三角形的性质即可求解.

（1）在△CEF中，∠ECF+∠CFE+∠CEF=180°，

∵∠CFE＝∠B

∴∠ECF+∠B+∠CEF=180°，

在△BCD中，∠BCD+∠B+∠CDB=180°，

∴∠AEC＝∠CDB；

（2）∵CG⊥AC,BC⊥CD,

∴∠ACG=∠BCD=90°，

∴∠ACD=∠BCG,

∵∠ACD+∠B=∠CAB，

∴∠BCG +∠B=∠CAB

∴∠AGC=∠B+∠BCG，

∴∠CAB=∠AGC

∴AC=AG;

（3）如图3，过点C作CH⊥AB于H，过点A作AP⊥AB与BC的延长线交于点P，过点C作CQ⊥AP于Q，

∴四边形AHCQ是矩形，

∴∠HCQ=90°，

由（2）知，AC=CG,∠ACG=90°，

∴CH=AH，

∴矩形AHCQ是正方形，

∴CH=CQ,

∵∠HCQ=90°，

∴∠PCQ+∠BCH=90°，

∵∠BCD=90°，

∴∠DCH+∠BCH=90°

∴∠PCQ=∠DCH

∵∠CQP=∠CHD=90°，

∴△CQP≌△CHD（ASA），

∴∠CPQ=∠CDH，CP=CD,

∵CD+CE=AE,

∴CP+CE=AE,

∴PE=AE,

∴∠P=∠PAE,

根据（1）可知∠AEC＝∠CDB

∵∠CPQ=∠CDH,

∴∠AEC=∠P=∠PAE,

∴∠P=60°，

∴∠B=90°-∠P=30°，

在Rt△CHG中，CH==1，

在Rt△CHB中，BC=2CH=2.