题目内容

【题目】如图，四边形ABCD的两条对角线AC、BD互相垂直， A1B1C1D1, 是四边形ABCD的中点四边形，如果AC=8, BD=10,那么四边形A1B1C1D1,的面积为_________.

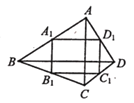
【答案】20

【解析】

此题要能够根据三角形的中位线定理证明四边形A1B1C1D1是矩形，从而根据矩形的面积进行计算．

解：∵A1，B1，C1，D1是四边形ABCD的中点四边形，且AC=8，BD=10

∴A1D1是△ABD的中位线

∴A1D1=0.5BD=0.5×10=5

同理可得A1B1=0.5AC=4

根据三角形的中位线定理，可以证明四边形A1B1C1D1是矩形

那么四边形A1B1C1D1的面积为A1D1×A1B1=5×4=20，故答案为：20.

练习册系列答案
相关题目

【题目】（1）探索材料1（填空）：

数轴上表示数和数的两点之间的距离等于．例如数轴上表示数2和5的两点距离为 ；数轴上表示数3和-1的两点距离为 ；则的意义可理解为数轴上表示数 和 这两点的距离；的意义可理解为数轴上表示数 和 这两点的距离；

（2）探索材料2（填空）：

①如图1，在工厂的一条流水线上有两个加工点和，要在流水线上设一个材料供应点往两个加工点输送材料，材料供应点应设在 才能使到的距离与到的距离之和最小？

②如图2，在工厂的一条流水线上有三个加工点要在流水线上设一个材料供应点往三个加工点输送材料，材料供应点应设在 才能使到三点的距离之和最小？

③如图3，在工厂的一条流水线上有四个加工点，要在流水线上设一个材料供应点往四个加工点输送材料，材料供应点应设在 才能使到四点的距离之和最小？

（3）结论应用（填空）：

①代数式的最小值是 ，此时的范围是 ；

②代数式的最小值是 ，此时的值为 ．

③代数式的最小值是 ，此时的范围是 ．

【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题，部分思路如下：如图，在∠ACB内做∠BCD＝∠B，CD与AB相交于点D，……．请根据以上思路，完成证明．

【题目】如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆．

（1）求证：AC是⊙O的切线；

（2）已知⊙O的半径为2.5，BE=4，求BC，AD的长．

【题目】在△ABC中，D、E分别是边AB、BC上的点，AE和CD交于点F，且∠CFE＝∠B。

（1）如图1，求证：∠AEC＝∠CDB；

（2）如图2，过点C作CG⊥AC，交AB于点G，CD⊥CB，∠ACD ＝∠CAB－∠B，求证：AC＝GC；

（3）如图3，在（2）的条件下，CE＋CD＝AE，CG＝，求线段BC的长。

【题目】已知△ABC中，AB=10，AC=2，∠B=30°，则△ABC的面积等于_____．

【题目】如图，平面直角坐标系中，已知点B的坐标为（6，4）．

（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）

（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．

【题目】（3分）以下四种沿AB折叠的方法中，不一定能判定纸带两条边线a，b互相平行的是（ ）

A. 如图1，展开后测得∠1=∠2

B. 如图2，展开后测得∠1=∠2且∠3=∠4

C. 如图3，测得∠1=∠2

D. 如图4，展开后再沿CD折叠，两条折痕的交点为O，测得OA=OB，OC=OD

【题目】为了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘成如图所示的频数分布直方图，己知成绩x（单位：分）均满足“50≤x＜100”．根据图中信息回答下列问题：

（1）图中a的值为　 　；

（2）若要绘制该样本的扇形统计图，则成绩x在“70≤x＜80”所对应扇形的圆心角度数为　 　度；

（3）此次比赛共有300名学生参加，若将“x≥80”的成绩记为“优秀”，则获得“优秀“的学生大约有　 　人：

（4）在这些抽查的样本中，小明的成绩为92分，若从成绩在“50≤x＜60”和“90≤x＜100”的学生中任选2人，请用列表或画树状图的方法，求小明被选中的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网