题目内容
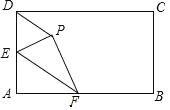
【题目】如图,点D、E在△ABC的BC边上,BD=CE,AD=AE。

(1)如图1,求证:∠BAD=∠CAE;
(2)如图2,若点E在AC的垂直平分线上,∠C=36°,直接写出图中所有的等腰三角形。
【答案】(1)见解析(2)△ABC,△ABD,△ADE,△ACE,△ACD,△ABE
【解析】
(1)根据AD=AE得到△ADE是等腰三角形,得到∠ADE=∠AED,根据平角的性质得到∠ADB=∠AEC,又BD=CE,可证明△ADB≌△AEC,故可求解;
(2)由(1)可得AB=AC,根据点E在AC的垂直平分线上得到AE=CE,故AD=DE,根据等腰三角形的定义即可写出.
(1)∵AD=AE
∴△ADE是等腰三角形,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
又BD=CE,
∴△ADB≌△AEC
∴∠BAD=∠CAE;
(2)∵△ADB≌△AEC
∴AB=AC,
∵点E在AC的垂直平分线上
∴AE=CE,∴BD=AD
∵∠C=36°,∴∠AED=2∠C=72°,
∴ADE=72°,
∴∠DAE=180°-2∠AED=36°,
∴∠CAD=∠DAE+∠CAE=72°,
∴AC=CD
同理AB=BE
∴图中的等腰三角形有△ABC,△ABD,△ADE,△ACE,△ACD,△ABE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目