题目内容
【题目】已知△ABC中，∠ACB ＝90°，∠A＝30°，点D在直线AC上，CD＝CB，点E在线段AC上，AE＝2EC，连接EB、BD，则∠EBD＝____________
【答案】15°或75°.
【解析】
根据题意，分情况作出图形，根据含30°的直角三角形特点分别进行计算即可.
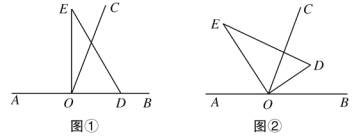
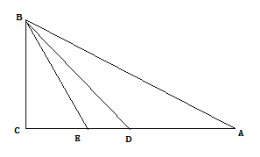
如图，①点D在线段AC上，设BC为1，∴CD=1
∵∠ACB ＝90°，∠A＝30°，
∴AB=2，AC=
，∠CBD=45°，
∵AE＝2EC
∴CE=
AC=
∴BE=
=
∴∠CBE=30°，
∴∠EBD=∠CBD-∠CBE=15°；
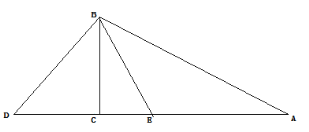
如图，②点D在直线AC上，设BC为1，∴CD=1
∵∠ACB ＝90°，∠A＝30°，
∴AB=2，AC=，∠CBD=45°，
∵AE＝2EC
∴CE=AC=
∴BE==
∴∠CBE=30°，
∴∠EBD=∠CBD+∠CBE=75°；
故填：15°或75°.
练习册系列答案
智慧小复习系列答案
相关题目
