��Ŀ����
����Ŀ��ij��ѧ���������40�����ʵ��������һ�����꾭Ӫ���˽һ�ֳɱ�Ϊ20Ԫ/����������Ʒ�ڵ�x�����۵������Ϣ���±���ʾ��
������p������ | P=50��x |
| ��1��x��20ʱ�� |
��1�������ڼ������Ʒ�����۵���Ϊ35Ԫ/����
��2����������x���õ�����y����x�ĺ�����ϵʽ��
��3����40���и�����ڼ����õ����������������Ƕ��٣�
���𰸡���1����10����25�����Ʒ�����۵���Ϊ35Ԫ/����2��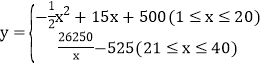 ��3����40���и������21���õ�����������������725Ԫ
��3����40���и������21���õ�����������������725Ԫ
��������
�⣺��1����1��x��20ʱ����![]() ����ã�
����ã�![]() ��
��
��21��x��40ʱ����![]() ����ã�
����ã�![]() ��
��
����10����25�����Ʒ�����۵���Ϊ35Ԫ/����
��2����1��x��20ʱ��![]() ��
��
��21��x��40ʱ��![]() ��
��
��y����x�ĺ�����ϵʽΪ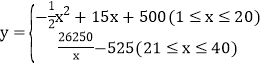 ��
��
��3����1��x��20ʱ��![]() ��
��
��![]() ������x=15ʱ��y�����ֵy1����y1=612.5��
������x=15ʱ��y�����ֵy1����y1=612.5��
��21��x��40ʱ����26250��0����![]() ����x���������С��
����x�����������
����x=21ʱ��![]() �����ֵy2����
�����ֵy2����![]() ��
��
��y1��y2��
����40���и������21���õ�����������������725Ԫ��
��1���ֱ�q=35�������۵��۹���x�ĺ�����ϵʽ�����x���ɡ�
��2��Ӧ������=�������룭���۳ɱ���ʽ���ɡ�
��3��Ӧ�ö��κ����ͷ��������������ʣ��ֱ�������ֵ�Ƚϼ�������