题目内容
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,将△ABC绕点A逆时针旋转α度(30<α<150)得到△AB′C′,B、C两点的对应点分别为点B′、C′,连接BC′,BC与AC、AB′相交于点E、F.
(1)当α=70时,∠ABC′=_____°,∠ACB′=______°.
(2)求证:BC′∥CB′.
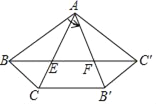
【答案】(1)40,70;(2)证明见解析.
【解析】
(1)由旋转的性质可得AB=AC=AB'=AC',∠CAC'=70°,∠B'AC'=∠BAC=30°,由等腰三角形的性质可求解;
(2)由旋转的性质和等腰三角形的性质可得∠ABC'=![]() ,∠ACB'=
,∠ACB'=![]() ,由三角形的外角性质可得∠AEF=
,由三角形的外角性质可得∠AEF=![]() =∠ACB',即可得BC'∥CB'.
=∠ACB',即可得BC'∥CB'.
(1)∵将△ABC绕点A逆时针旋转α度得到△AB′C′,且AB=AC,∠BAC=30°,
∴AB=AC=AB'=AC',∠CAC'=70°,∠B'AC'=∠BAC=30°,
∴∠BAC'=100°,且AB=AC',
∴∠ABC'=40°,
∵∠CAB'=∠CAC'﹣∠B'AC'=40°,且AC=AB'
∴∠ACB'=70°
故答案为40,70
(2)∵将△ABC绕点A逆时针旋转α度得到△AB′C′,且AB=AC,∠BAC=30°,
∴AB=AC=AB'=AC',∠CAC'=α,∠B'AC'=∠BAC=30°,
∴∠BAC'=30°+α,∠CAB'=α﹣30°,且AB=AC=AB'=AC',
∴∠ABC'=![]() ,∠ACB'=
,∠ACB'=![]()
∵∠AEF=∠ABE+∠BAC
∴∠AEF=![]()
∴∠AEF=∠ACB',
∴BC'∥B'C

【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示。
销售量p(件) | P=50—x |
| 当1≤x≤20时, |
(1)请计算第几天该商品的销售单价为35元/件?
(2)求该网店第x天获得的利润y关于x的函数关系式。
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?