题目内容
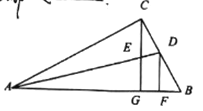
【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°. 
(1)AB与DE平行吗?请说明理由;
(2)若DC是∠NDE的平分线.
①试说明∠ABC=∠C;
②试说明BD是∠ABC的平分线.
(要求:第(1)小题要写出每一步的理由,第(2)小题的理由可省略不写.)
【答案】
(1)解:AB∥DE,理由如下:
∵MN∥BC(已知),
∴∠ABC=∠1=60°(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠ABC=∠2(等量代换),
∴AB∥DE(同位角相等,两直线平行)
(2)解:①∵MN∥BC,
∴∠1=∠ABC=60°,∠NDE+∠2=180°,
∴∠NDE=180°﹣∠2=180°﹣60°=120°,
∵DC是∠NDE的平分线,
∴∠EDC=∠NDC= ![]() ∠NDE=60°,
∠NDE=60°,
∵MN∥BC,
∴∠C=∠NDC=60°,
∴∠ABC=∠C;
②∠ADC=180°﹣∠NDC=180°﹣60°=120°,
∵BD⊥DC,
∴∠BDC=90°,
∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°,
∵MN∥BC,
∴∠DBC=∠ADB=30°,
∴∠ABD=∠DBC= ![]() ∠ABC,
∠ABC,
∴BD是∠ABC的平分线
【解析】(1)根据平行线的性质得出∠ABC=∠1=60°,求出∠ABC=∠2,根据平行线的判定得出即可;(2)①根据平行线的性质得出∠1=∠ABC=60°,∠NDE+∠2=180°,求出∠EDC=∠NDC= ![]() ∠NDE=60°,根据平行线的性质得出∠C=∠NDC=60°,即可得出答案;②求出∠ADC=120°,求出∠ADB=30°,根据平行线的性质求出∠DBC=∠ADB=30°,即可得出答案.
∠NDE=60°,根据平行线的性质得出∠C=∠NDC=60°,即可得出答案;②求出∠ADC=120°,求出∠ADB=30°,根据平行线的性质求出∠DBC=∠ADB=30°,即可得出答案.
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案