题目内容
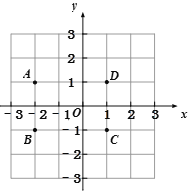
【题目】探究:如图1,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数y= ![]() (k>0,x>0)的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(k>0,x>0)的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(1)若 ![]() ,请用含n的代数式表示
,请用含n的代数式表示 ![]() ;
;
(2)求证:AC=BD;
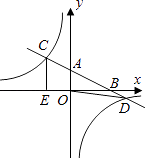
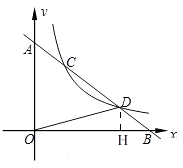
应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数y= ![]() (k>0,x>0)的图象交于点C,D两点(点C在点D的左边),已知
(k>0,x>0)的图象交于点C,D两点(点C在点D的左边),已知 ![]() ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
【答案】
(1)解:∵∠ACE=∠DCG,∠AEC=∠DGC=90°,
∴△ACE∽△DCG
∴ ![]()
(2)解:∵G(a,b)
∴C( ![]() ) D(a,
) D(a, ![]() ),
),
∴EC= ![]() ,CG=a﹣
,CG=a﹣ ![]() ,DF=
,DF= ![]() ,DG=b﹣
,DG=b﹣ ![]() ,
,
∴ 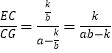 ,
, 
由(1)知,△ACE∽△DCG,
∴ ![]() =
= ![]() ,
,
同理:△DCG∽△DBF,
∴ ![]() ,
,
即△ACE与△DBF都和△DCG相似,且相似比都为 ![]() ,
,
∴△ACE≌△DBF
∴AC=BD,
应用:如图,过点D作DH⊥x轴于点H
由(2)可得AC=BD
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]() ,
,
∴ 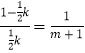 ,
,
∴ ![]() .
.
【解析】(1)利用两角相等的两三角形相似即可得出结论;(2)先求出 ![]() ,
, ![]() ,进而判断出△ACE≌△DBF即可得出结论;
,进而判断出△ACE≌△DBF即可得出结论;
应用:先求出 ![]() ,进而得出
,进而得出 ![]() ,即可得出结论.
,即可得出结论.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表, 
请回答下列问题:
七年级兴趣班报名情况统计表.
兴趣班名称 | 频率 |
“无人机” | a |
“3D打印” | 0.05 |
“网页设计” | 0.25 |
“电脑绘画” | 0.40 |
(1)报名参加兴趣班的总人数为人;统计表中的a=;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?