��Ŀ����
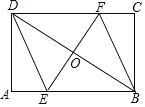
����Ŀ����ͼ������������MNPQ�У�ÿ��С����ı߳�����ȣ�������ABCD�Ķ�����������MNPQ��4���ߵ�С�����ϣ�

(1)��������MNPQ�����ڵ�ÿ��С����ı߳�Ϊ1����
�١�ABQ����BCM����CDN����ADP�������
��������ABCD�������
(2)��MB��a��BQ��b���������ͼ���е�ֱ�������κ������ε������ϵ��������֤��ѧ������һ����ѧ��ʽ������
���𰸡���1����S��ABQ��6�� S��BCM��6�� S��CDN��6�� S��ADP��6����S������ABCD��25����2����֤�˹��ɶ�����֤�������������.
��������
��1���ٸ���ֱ�������ε������ʽ���ɵó������
��������ó�S������ABCD=S������MNPQ��4S��ABQ�����ɵó������
��2����Ȼ��������ܹ���֤���ɶ�����
��1���١�������ÿ��С�����εı߳�Ϊ1����ͼ��֪AQ=3��BQ=4����Q=90�㣬��S��ABQ![]() AQBQ=6��ͬ��S��BCM=S��CDN=S��ADP=6��
AQBQ=6��ͬ��S��BCM=S��CDN=S��ADP=6��
�ڡ�MQ=7����S������MNPQ=72=49����S������ABCD=S������MNPQ��4S��ABQ=49��4��6=25��
��2����֤���ɶ�����
��֤���ڡ�BCM�͡�ABQ�У���BM=AQ����M=��Q��CM=BQ�����BCM�ա�ABQ��SAS����ͬ����CDN�ա�DAP�ա�BCM��
��S������ABCD=S������MNPQ��4S��ABQ
��AB2=��a+b��2��4![]() ab����AB2=a2+b2��
ab����AB2=a2+b2��
��AB=c���ã�c2=a2+b2�����ɶ�������

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�����Ŀ��ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ����������ֻ����ɲ�������15.5��Ԫ��Ԥ��ȫ�����ۺ�ɻ�ë����2.1��Ԫ��
��ë����=���ۼ۩����ۣ�����������
��1�����̳��ƻ������ס��������ֻ������ٲ���
��2��ͨ���г����У����̳�������ԭ�ƻ��Ļ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����
����Ŀ��ij������ʦ����˶��ֻ����п��߶��������ζ�����������������һ�ζ�����ȣ�����ʦ�ڶ��ζ������������İٷ�������ƽ���������ٵİٷ��ʵ�3����������ʦ�ڶ��ζ���ʱƽ���������ٵİٷ���Ϊx��0��x��0.5����
��Ŀ | ��һ�ζ��� | �ڶ��ζ��� |
���������� | 10000 | �� |
ƽ����������/���� | 0.6 | �� |
���루�ף� | 6000 | 7020 |
ע��������ƽ������=���룮
��1������������ɱ�����գ�
��2����x��
��3������ʦ���ֺ����в���������һΪ24000������������ζ���������������500�ף�ʹ���ܲ���ǡ��Ϊ24000����������ʦ��500��ƽ��������