题目内容
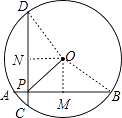
【题目】如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为 . 
【答案】3 ![]()
【解析】解:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,∵AB=CD=8,
∴BM=DN=4,
∴OM=ON= ![]() =3,
=3,
∵AB⊥CD,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=3 ![]() .
.
所以答案是:3 ![]() .
.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目





