题目内容
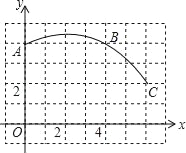
【题目】如图,抛物线![]() 与x轴交于A、B两点,与
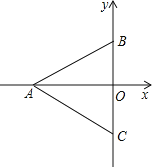
与x轴交于A、B两点,与![]() 轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.
轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.

(1)求抛物线所对应的函数解析式.
(2)若点P为抛物线对称轴上的一个动点,求![]() PAC周长的最小值.
PAC周长的最小值.
(3)将AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
【答案】(1)![]() ,(2)
,(2)![]() ,(3)点G不在该抛物线上.
,(3)点G不在该抛物线上.
【解析】
(1)利用矩形的性质得出E,C点坐标,进而利用待定系数法求二次函数解析式;
(2)先根据题意得出直线AE与对称轴的交点为点P时,△PAC的周长最小,再求出AC+AE的值即可;
(3)首先根据旋转条件求出G点的坐标,然后将点G的坐标代入抛物线的解析式中直接进行判定即可.
(1)∵四边形OCEF为矩形,且OF=2,EF=3,
∴C点坐标为:(0,3),E点坐标为:(2,3),
将C,E代入y=-x2+bx+c得:
![]() ,
,
解得:![]() ,
,
∴抛物线对应的函数解析式为:y=-x2+2x+3;
(2)∵y=-x2+2x+3,
∴A(-1,0),
∴AF=3,
由于点C、E关于抛物线对称轴对称,
∴取直线AE与对称轴的交点为点P时,
△PAC的周长最小,
△PAC周长=AC+AE=![]() +
+![]() =
=![]() +
+![]() =
=![]() .
.
(3)点G不在该抛物线上.
根据题意,![]() 绕点C逆时针旋转
绕点C逆时针旋转![]() ,
,![]() 落在
落在![]() 所在的直线上,
所在的直线上,
由(2)可知![]() ,
,
∴点A对应点G的坐标为![]() ,
,
当![]() 时,
时,![]() ,
,
所以点G不在该抛物线上.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目