题目内容
【题目】(1)观察猜想
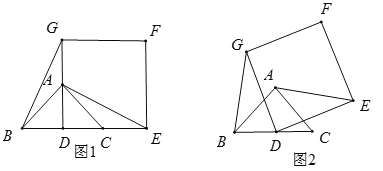
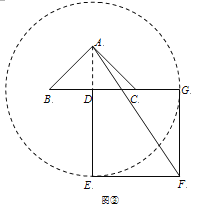
如图(1),在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点.以点D为顶点作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG,则线段BG和AE的数量关系是_____;
(2)拓展探究
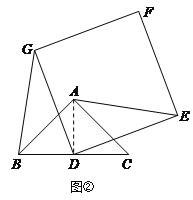
将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图2,则(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
(3)解决问题
若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,直接写出AF的值.
【答案】(1)BG=AE.
(2)成立.
如图②,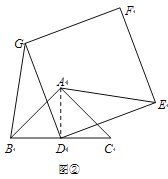
连接AD.∵△ABC是等腰三直角角形,∠BAC=90°,点D是BC的中点.
∴∠ADB=90°,且BD=AD.
∵∠BDG=∠ADB-∠ADG=90°-∠ADG=∠ADE,DG=DE.
∴△BDG≌△ADE,∴BG=AE.…………………………………………7分
(3)由(2)知,BG=AE,故当BG最大时,AE也最大.
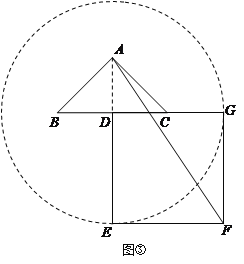
正方形DEFG绕点D逆时针方向旋转270°时,BG最大,如图③.
若BC=DE=2,则AD=1,EF=2.
在Rt△AEF中,AF2=AE2+EF2=(AD+DE)2+EF2=(1+2)2+22=13.
∴AF=![]()
【解析】
解:(1)BG=AE.
(2)成立.
如图②,连接AD.
∵△ABC是等腰三直角角形,∠BAC=90°,点D是BC的中点.
∴∠ADB=90°,且BD=AD.
∵∠BDG=∠ADB-∠ADG=90°-∠ADG=∠ADE,DG=DE.
∴△BDG≌△ADE,∴BG=AE.
(3)由(2)知,BG=AE,故当BG最大时,AE也最大.Z+X+X+K]
因为正方形DEFG在绕点D旋转的过程中,G点运动的图形是以点D为圆心,DG为半径的圆,故当正方形DEFG旋转到G点位于BC的延长线上(即正方形DEFG绕点D逆时针方向旋转270°)时,BG最大,如图③.
若BC=DE=2,则AD=1,EF=2.
在Rt△AEF中,AF2=AE2+EF2=(AD+DE)2+EF2=(1+2)2+22=13.
∴AF=![]() .
.
即在正方形DEFG旋转过程中,当AE为最大值时,AF=![]() .
.

 科学实验活动册系列答案
科学实验活动册系列答案