题目内容
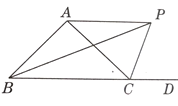
【题目】今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队及时联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=﹣![]() x+m(m为常数).
x+m(m为常数).
(1)求该企业月生产量y(千件)与出厂价x(元)之间的函数关系式,并写出自变量x的取值范围.
(2)当该企业生产出的产品出厂价定为多少元时,月利润W(元)最大?最大利润是多少?[月利润=(出厂价﹣成本)×月生产量﹣工人月最低工资].

【答案】(1)y=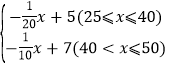 ;(2)45, 最大利润是45元.
;(2)45, 最大利润是45元.
【解析】试题分析:(1)把(40,3)代入y=-![]() x+m得,3=-
x+m得,3=-![]() ×40+m,求得y=-
×40+m,求得y=-![]() x+5,(25≤x≤40),设BC的解析式为:y=kx+b,把(40,3),(50,2)代入y=kx+b得得到y=-
x+5,(25≤x≤40),设BC的解析式为:y=kx+b,把(40,3),(50,2)代入y=kx+b得得到y=-![]() x+7,(40<x≤50);
x+7,(40<x≤50);
(2)设该企业生产出的产品出厂价定为x元时,月利润W(元)最大,根据题意得到二次函数的解析式,求得当x=40时,W最大=30299元,当x=45时,W最大=32342.5元,即可得到结论.
(1)把(40,3)代入y=![]() x+m得,3=
x+m得,3=![]() ×40+m,
×40+m,
∴m=5,
∴y=![]() x+5,(25x40),
x+5,(25x40),
设BC的解析式为:y=kx+b,
把(40,3),(50,2)代入y=kx+b得,![]() ,
,
解得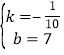 ,
,
∴y=110x+7,(40<x50),
综上所述:y=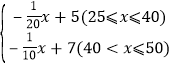 ;
;
(2)设该企业生产出的产品出厂价定为x元时,月利润W(元)最大,
根据题意得,W=(![]() x+5)(x20)32000=
x+5)(x20)32000=![]() x2+6x32100=120(x60)2+33900,
x2+6x32100=120(x60)2+33900,
∵25x40,
∴当x=40时,W最大=30299元,
W=(![]() x+7)(x20)32000=
x+7)(x20)32000=![]() x2+9x32140=
x2+9x32140=![]() (x45)+32342.5,
(x45)+32342.5,
∵40<x50,
∴当x=45时,W最大=32342.5元,
∵30299<32342.5,
∴当该企业生产出的产品出厂价定为45元时,月利润W(元)最大,最大利润是34342.5元。

 阅读快车系列答案
阅读快车系列答案