题目内容
【题目】甲、乙两车从
地出发，匀速驶向
地，甲车行驶
后，乙车才以
的速度沿相同路线行驶，乙车先到达地并停留
后，再以原速按原路返回，直至与甲车相遇，在此过程中，两车之间的距离
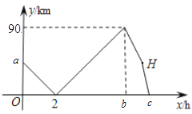
与乙车行驶时间
之间的函数关系如图所示，下列说法：①
；②
；③点
的坐标是
；④
，其中正确的有（ ）
A.4个B.3个C.2个D.1个
【答案】C
【解析】
设甲车的速度为
，由图像可知
时乙开始出发，此时甲乙相距
千米，所以为乙出发时甲所走的路程；当
时，甲乙间距离减小，到
时，甲乙间距离0，说明乙追上甲，由相遇时甲乙所走路程相同可求出v的值； 
时甲乙间距离增大，乙超过甲，在
时，距离最大为90km，由此可求出b的值；乙车在B地停留
到点H，求出此时甲乙的距离即为H点纵坐标；再以原速返回，在
时，距离再次为0，甲乙相遇，求出从乙开始返回到相遇所需时间，可得c的值.
解：设甲车的速度为，则
，解得
，
，①正确；
，解得
，②正确；因为乙车到达
地并停留，所以H点的横坐标为5.5，甲在乙停留的时间走的路程为
，
，所以此时甲乙相距60km，即点H的纵坐标为60，所以点
的坐标是
，③错误；由③知此时甲乙相距60km，设t时后甲乙相遇，则
，解得
，所以
，④错误，其中正确的有两个.
故选：C
【题目】某校计划建一间多功能数学实验室，将采购两类桌椅：A类是三角形桌，每桌可坐3人，B类是五边形桌，每桌可坐5人．学校拟选择甲、乙两家公司中的一家来采购，两家公司的标价均相同，且规定两类桌椅均只能在同一家公司采购．甲公司对两类桌椅均是以标价出售；乙公司对A类桌椅涨价20%、B类桌椅降价20%出售．经咨询，两家公司给出的数量和费用如下表：
A类桌椅（套） | B类桌椅（套） | 总费用（元） | |
甲公司 | 6 | 5 | 1900 |
乙公司 | 3 | 7 | 1660 |
（1）求第一次购买时，A、B两类桌椅每套的价格分别是多少？
（2）如果该数学实验室需设置48个座位，学校到甲公司采购，应分别采购A、B两类桌椅各多少套时所需费用最少？
