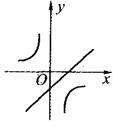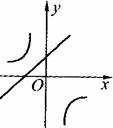题目内容
已知抛物线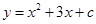 过两点(m,0)、(n,0),且
过两点(m,0)、(n,0),且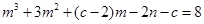 ,抛物线于双曲线
,抛物线于双曲线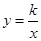 (x>0)的交点为(1,d).
(x>0)的交点为(1,d).
(1)求抛物线与双曲线的解析式;
(2)已知点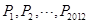 都在双曲线
都在双曲线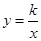 (x>0)上,它们的横坐标分别为
(x>0)上,它们的横坐标分别为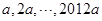 ,O为坐标原点,记
,O为坐标原点,记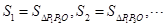 ,点Q在双曲线
,点Q在双曲线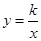 (x<0)上,过Q作QM⊥y轴于M,记
(x<0)上,过Q作QM⊥y轴于M,记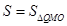 。
。
求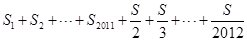 的值.
的值.
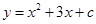 过两点(m,0)、(n,0),且
过两点(m,0)、(n,0),且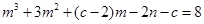 ,抛物线于双曲线
,抛物线于双曲线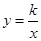 (x>0)的交点为(1,d).
(x>0)的交点为(1,d).(1)求抛物线与双曲线的解析式;
(2)已知点
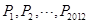 都在双曲线
都在双曲线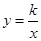 (x>0)上,它们的横坐标分别为
(x>0)上,它们的横坐标分别为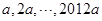 ,O为坐标原点,记
,O为坐标原点,记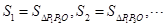 ,点Q在双曲线
,点Q在双曲线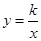 (x<0)上,过Q作QM⊥y轴于M,记
(x<0)上,过Q作QM⊥y轴于M,记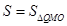 。
。求
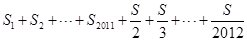 的值.
的值.(1)抛物线为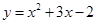 ,曲线的解析式
,曲线的解析式 ;(2)2025077.
;(2)2025077.
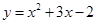 ,曲线的解析式
,曲线的解析式 ;(2)2025077.
;(2)2025077.试题分析:(1)将(m,0)(n,0)代入抛物线,组成方程组求解即可.
(2)由点都在双曲线上,可以总结出点的坐标,用a表示,得出规律,求三角形的面积,然后相加即可.
试题解析:
(1)
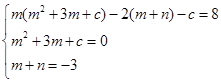 解之得c=-2
解之得c=-2∴
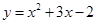
由
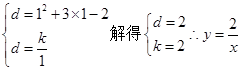
(2)∵点
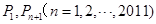 都在双曲线
都在双曲线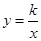 (x>0)上,它们的横坐标分别为
(x>0)上,它们的横坐标分别为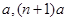 ,∴点
,∴点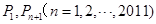 的纵坐标为
的纵坐标为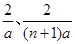 。
。如图,过
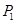 、
、 分别作x轴、y轴的平行线
分别作x轴、y轴的平行线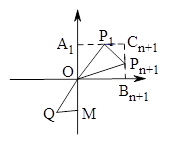
则
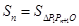 =
=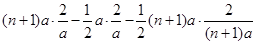
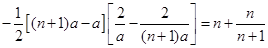
Q在双曲线
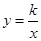 上,易求
上,易求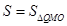 =1.
=1.所以
 =(1+
=(1+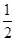 )+(2+
)+(2+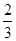 )+ …+(2011+
)+ …+(2011+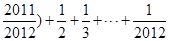 =1+2+…+2011+1×2011=2025077.
=1+2+…+2011+1×2011=2025077.
练习册系列答案
相关题目
 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.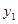 )、B(-2,
)、B(-2,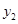 )、C(3,
)、C(3,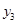 )在抛物线
)在抛物线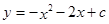 上,则
上,则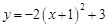 的顶点坐标是
的顶点坐标是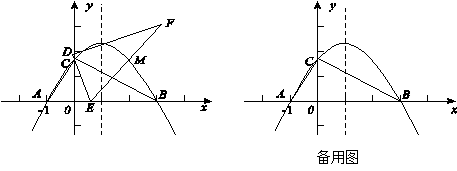
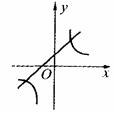
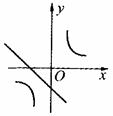
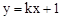 与
与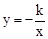 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )