题目内容
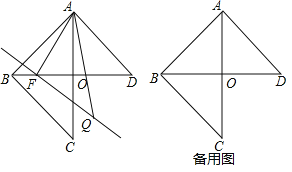
【题目】如图,已知![]() 为
为![]() 的高线,
的高线,![]() ,以
,以![]() 为底边作等腰
为底边作等腰![]() ,连接
,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于
于![]() 点,下列结论:①
点,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 为等腰三角形;⑤
为等腰三角形;⑤![]() ,其中正确的有( )
,其中正确的有( )
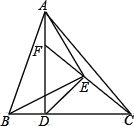
A.①③B.①②④C.①③④D.①②③⑤
【答案】D
【解析】
①根据等腰直角三角形的性质即可证明∠CBE=∠DAE,再得到△ADE≌△BCE;
②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;
③证明△AEF≌△BED即可;
④根据△AEF≌△BED得到DE=EF, 又DE⊥CF,故可判断;
⑤易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
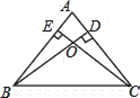
①∵AD为△ABC的高线,
∴CBE+∠ABE+∠BAD=90°,
∵Rt△ABE是等腰直角三角形,
∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,
∴∠CBE+∠BAD=45°,
∴∠DAE=∠CBE,故①正确;
在△DAE和△CBE中,
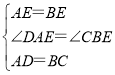 ,
,
∴△ADE≌△BCE(SAS);
②∵△ADE≌△BCE,
∴∠EDA=∠ECB,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠ECB=90°,
∴∠DEC=90°,
∴CE⊥DE;
故②正确;
③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,
∴∠BDE=∠AFE,
∵∠BED+∠BEF=∠AEF+∠BEF=90°,
∴∠BED=∠AEF,
在△AEF和△BED中,
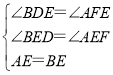 ,
,
∴△AEF≌△BED(AAS),
∴BD=AF
故③正确;
∵△AEF≌△BED
∴DE=EF, 又DE⊥CF,
∴△DEF为等腰直角三角形,故④错误;
④∵AD=BC,BD=AF,
∴CD=DF,
∵AD⊥BC,
∴△FDC是等腰直角三角形,
∵DE⊥CE,
∴EF=CE,
∴S△AEF=S△ACE,
∵△AEF≌△BED,
∴S△AEF=S△BED,
∴S△BDE=S△ACE.
故④正确;
故选:D.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】某水果超市为了吸引顾客来店购物,设立了一个如图所示的可以自由转动的转盘,开展有奖购物活动.顾客购买商品满200元就能获得一次转动转盘的机会,当转盘停止时,指针落在“一袋苹果”的区域就可以获得“一袋苹果”的奖品;指针落在“一盒樱桃”的区域就可以获得“一盒樱桃”的奖品.下表是该活动的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“一袋苹果”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“一袋苹果”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
下列说法不正确的是( )

A. 当n很大时,估计指针落在“一袋苹果”区域的频率大约是0.70
B. 假如你去转动转盘一次,获得“一袋苹果”的概率大约是0.70
C. 如果转动转盘2000次,指针落在“一盒樱桃”区域的次数大约有600次
D. 转动转盘10次,一定有3次获得“一盒樱桃”