题目内容
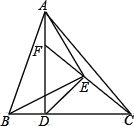
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于
于![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求证:
,求证:
![]() ;
;
![]() ;
;
![]() 是等腰直角三角形.
是等腰直角三角形.

【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)取AB中点M,连接ME,利用正方形的性质和等腰直角三角形的性质,证得△AME≌△ECF,得出结论;
(2)利用(1)图,△AEF是等腰直角三角形,∠2=∠4,∠ACF=∠B,证得结论;
(3)设正方形ABCD边长为2a,则BE=a,过F作FN⊥BC的延长线于N,FP⊥CD于P,证得四边形PCNF是矩形,△FCN是等腰直角三角形,△FNE≌△EBA(AAS),得到FN=BE=a,进而得到DC=FC,即可得到△DFC是等腰直角三角形.
(1)如图(1),取AB中点M,连接ME,则AM=BM=BE=CE=![]() BC,∴在Rt△BME中,∠BME=∠BEM=45°,∴∠AME=135°,∠1+∠2=45°.
BC,∴在Rt△BME中,∠BME=∠BEM=45°,∴∠AME=135°,∠1+∠2=45°.
∵∠AEF=90°,∴∠1+∠3=45°,∴∠2=∠3.
∵CF是正方形外角的平分线,∴∠DCF=![]() ×90°=45°,∴∠ECF=90°+45°=∠AME.
×90°=45°,∴∠ECF=90°+45°=∠AME.
在△AME和△ECF中,∵ ,∴△AME≌△ECF(ASA),∴AE=EF.
,∴△AME≌△ECF(ASA),∴AE=EF.

(2)如图(1).∵∠AEF=90°,AE=EF,∴△AEF是等腰直角三角形,∴∠EAF=45°,即∠4+∠5=45°.
∵AC为正方形ABCD的对角线,∴∠BAC=45°,即∠2+∠5=45°,∴∠2=∠4.
∵∠DCF=∠DCA=![]() ×90°=45°,∴∠ACF=45°+45°=90°=∠B,∴△ABE∽△ACF.
×90°=45°,∴∠ACF=45°+45°=90°=∠B,∴△ABE∽△ACF.
(3)如图(2),设正方形ABCD边长为2a,则BE=a,AE=EF=![]() a.
a.
∵△AEF是等腰直角三角形,∴AF=![]() AE=
AE=![]() a.
a.
过F作FN⊥BC的延长线于N,FP⊥CD于P,则四边形PCNF是矩形,∠FNE=90°=∠B.
∵∠FCN=45°,∴△CNF是等腰直角三角形,∴CN=FN.
又由(1)知,∠3=∠2,EF=AE.在△FNE和△EBA中,∵ ,∴△FNE≌△EBA(AAS),∴FN=BE=a,∴PC=PF=CN=a,∴DP=a,∴DF=
,∴△FNE≌△EBA(AAS),∴FN=BE=a,∴PC=PF=CN=a,∴DP=a,∴DF=![]() =
=![]() ,∴DC=FC.
,∴DC=FC.
∵∠DCF=45°,∴∠CDF=45°,∴∠DFC=90°,∴△DFC是等腰直角三角形.