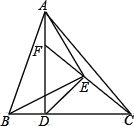
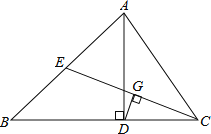
题目内容
【题目】已知在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 为线段
为线段![]() 上一动点,以每秒
上一动点,以每秒![]() 的速度从
的速度从![]() 匀速运动到
匀速运动到![]() ,过
,过![]() 作直线
作直线![]() ,且
,且![]() ,点
,点![]() 在直线
在直线![]() 的右侧,设点
的右侧,设点![]() 运动时间为
运动时间为![]() .
.
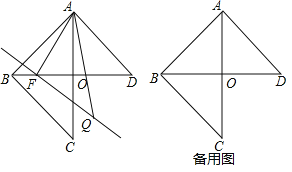
(1)当![]() 为等腰三角形时,
为等腰三角形时,![]() ;
;
(2)当![]() 点在线段
点在线段![]() 上时,过
上时,过![]() 点作
点作![]() 于点
于点![]() ,求证
,求证![]() ;
;
(3)当![]() 点在线段
点在线段![]() 上运动的过程中,
上运动的过程中,![]() 的面积是否变化?若不变,求出它的值.
的面积是否变化?若不变,求出它的值.
【答案】(1)3或6或![]() ;(2)见解析;(3)不变,S△ABQ=9.
;(2)见解析;(3)不变,S△ABQ=9.
【解析】
(1)分三种情况讨论,由等腰三角形的性质可求BF的长,即可求t的值;
(2)由等腰三角形的性质可得∠AOB=90°,由“AAS”可证△AOF≌△FHQ;
(3)由“AAS”可证△AOF≌△FHQ,可得OF=QH=t-3,由面积的和差关系可求解.
(1)∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°,
若AB=AF时,即点F与点D重合,
∴BF=BD=6cm,
∴t=![]() =6,
=6,
若BF=AF时,
∴∠ABF=∠BAF=45°,
∴∠AFB=90°,
∴AF⊥BD,且AB=AD
∴BF=DF=3cm,
∴t=![]() =3,
=3,
若AB=BF=![]() cm,
cm,
∴t=![]() =
=![]()
故答案为:3或6或![]() .
.
(2)如图1,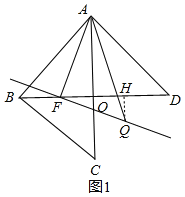
∵∠DAB=∠ABC=90°,AD=AB=CB,
∴∠ABD=∠ADB=45°,∠BAC=∠ACB=45°,
∴∠AOB=90°,
∵AF⊥FQ,QH⊥BD,
∴∠AFQ=∠FHQ=90°,
∴∠QFH+∠FQH=90°,∠AFO+∠QFH=90°,
∴∠AFO=∠FQH,AF=FQ,∠AOF=∠FHQ=90°
∴△AOF≌△FHQ(AAS)
(3)不变,
理由如下:如图2,过点Q作QH⊥BD,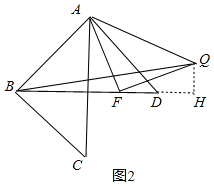
∵∠DAB=∠ABC=90°,AD=AB=CB,
∴∠ABD=∠ADB=45°,∠BAC=∠ACB=45°,
∴∠AOB=90°,
∵AF⊥FQ,QH⊥BD,
∴∠AFQ=∠FHQ=90°,
∴∠QFH+∠FQH=90°,∠AFO+∠QFH=90°,
∴∠AFO=∠FQH,AF=FQ,∠AOF=∠FHQ=90°
∴△AOF≌△FHQ(AAS)
∴OF=QH=t-3,
∵S△ABQ=S△ABF+S△AFQ-S△BFQ=![]() BF×AO+
BF×AO+![]() ×AF2-
×AF2-![]() ×BF×QH
×BF×QH
∴S△ABQ=![]() ×t×3+
×t×3+![]() [32+(t-3)2]-
[32+(t-3)2]-![]() ×t×(t-3)=9
×t×(t-3)=9
故△ABQ的面积不发生变化.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案