题目内容
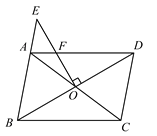
【题目】如图，O是正△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④S四边形AOBO
；⑤S△AOC+S△AOB=
．其中正确的结论是（ ）
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
【答案】A
【解析】
证明△BO′A≌△BOC，又∠OBO′=60°，所以△BO′A可以由△BOC绕点B逆时针旋转60°得到，故结论①正确；由△OBO′是等边三角形，可知结论②正确；在△AOO′中，三边长为3，4，5，这是一组勾股数，故△AOO′是直角三角形；进而求得∠AOB=150°，故结论③正确；S四边形AOBO=S△AOO+S△OBO，可得结论④错误；如图②，将△AOB绕点A逆时针旋转60°，使得AB与AC重合，点O旋转至O″点．利用旋转变换构造等边三角形与直角三角形，将S△AOC+S△AOB转化为S△COO+S△AOO，计算可得结论⑤正确．
由题意可知，∠1+∠2=∠3+∠2=60°，∴∠1=∠3，
又∵OB=O′B，AB=BC，
∴△BO′A≌△BOC，又∵∠OBO′=60°，
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到，
故结论①正确；
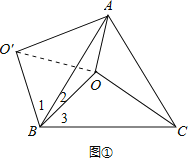
如图①，连接OO′，
∵OB=O′B，且∠OBO′=60°，
∴△OBO′是等边三角形，
∴OO′=OB=4．
故结论②正确；
∵△BO′A≌△BOC，∴O′A=5．
在△AOO′中，三边长为3，4，5，这是一组勾股数，
∴△AOO′是直角三角形，∠AOO′=90°，
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°，
故结论③正确；
S四边形AOBO′=S△AOO′+S△OBO′=
，
故结论④错误；
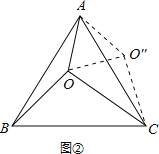
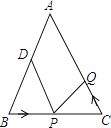
如图②所示，将△AOB绕点A逆时针旋转60°，使得AB与AC重合，点O旋转至O″点．
易知△AOO″是边长为3的等边三角形，△COO″是边长为3、4、5的直角三角形，
则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=
，
故结论⑤正确．
综上所述，正确的结论为：①②③⑤．
故选A．
