题目内容
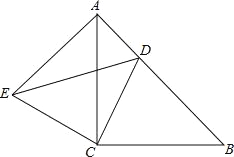
【题目】如图，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，
（1）求证：△ACE≌△BCD；
（2）若DE=13，BD=12，求线段AB的长．
【答案】（1）证明见解析; （2）AB=17.
【解析】
试题（1）由等腰直角三角形得出AC=BC，CE=CD，∠ACB=∠ECD=90°，得出∠BCD=∠ACE，根据SAS推出△ACE≌△BCD即可；
（2）求出AD=5，根据全等得出AE=BD=12，在Rt△AED中，由勾股定理求出DE即可．
试题解析：（1）∵△ACB与△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∵∠ACB=∠ECD=90°，∴∠ACB﹣∠ACD=∠DCE﹣∠ACD，∴∠BCD=∠ACE，在△BCD和△ACE中，∵BC=AC，∠BCD=∠ACE，CD=CE，∴△BCD≌△ACE（SAS）；
（2）由（1）知△BCD≌△ACE，则∠DBC=∠EAC，AE=BD=12，∵∠CAD+∠DBC=90°，∴∠EAC+∠CAD=90°，即∠EAD=90°，∵AE=12，ED=13，∴AD=
=5，∴AB=AD+BD=12+5=17．
【题目】为了打造区域中心城市，实现攀枝花跨越式发展，我市花城新区建设正按投资计划有序推进．花城新区建设工程部，因道路建设需要开挖土石方，计划每小时挖掘土石方540m3 ， 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如下表所示：
租金（单位：元/台时） | 挖掘土石方量（单位：m3/台时） | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
（1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？
（2）如果每小时支付的租金不超过850元，又恰好完成每小时的挖掘量，那么共有哪几种不同的租用方案？
