题目内容
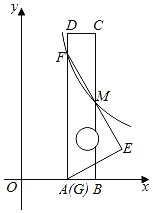
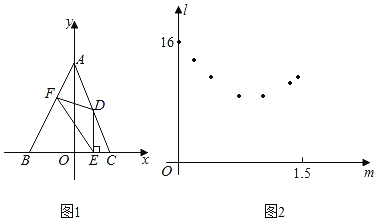
【题目】如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=﹣![]() x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值.
②△BEF能否成为直角三角形.
小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究,请你一起来解决问题.
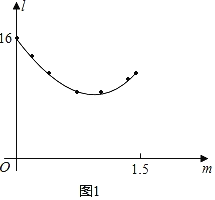
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
【答案】(1)连线见解析,二次函数;(2)![]() ;(3)m=0或m=
;(3)m=0或m=![]()
【解析】
(1)根据描点法画图即可;
(2)过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,证明Rt△FGK≌Rt△DHK(AAS),由全等三角形的性质得出FG=DH,可求出F(﹣m,﹣2m+4),根据勾股定理得出l=EF2=8m2﹣16m+16=8(m﹣1)2+8,由二次函数的性质可得出答案;
(3)分三种不同情况,根据直角三角形的性质得出m的方程,解方程求出m的值,则可求出答案.
解:(1)用描点法画出图形如图1,由图象可知函数类别为二次函数.
(2)如图2,过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,
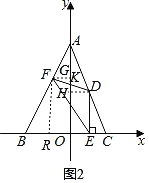
则∠FGK=∠DHK=90°,
记FD交y轴于点K,
∵D点与F点关于y轴上的K点成中心对称,
∴KF=KD,
∵∠FKG=∠DKH,
∴Rt△FGK≌Rt△DHK(AAS),
∴FG=DH,
∵直线AC的解析式为y=﹣![]() x+4,
x+4,
∴x=0时,y=4,
∴A(0,4),
又∵B(﹣2,0),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=2x+4,
过点F作FR⊥x轴于点R,
∵D点的橫坐标为m,
∴F(﹣m,﹣2m+4),
∴ER=2m,FR=﹣2m+4,
∵EF2=FR2+ER2,
∴l=EF2=8m2﹣16m+16=8(m﹣1)2+8,
令﹣![]() +4=0,得x=
+4=0,得x=![]() ,
,
∴0≤m≤![]() .
.
∴当m=1时,l的最小值为8,
∴EF的最小值为2![]() .
.
(3)①∠FBE为定角,不可能为直角.
②∠BEF=90°时,E点与O点重合,D点与A点,F点重合,此时m=0.
③如图3,∠BFE=90°时,有BF2+EF2=BE2.
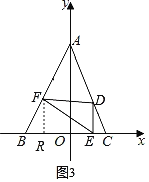
由(2)得EF2=8m2﹣16m+16,
又∵BR=﹣m+2,FR=﹣2m+4,
∴BF2=BR2+FR2=(﹣m+2)2+(﹣2m+4)2=5m2﹣20m+20,
又∵BE2=(m+2)2,
∴(5m2﹣20m+8)+(8m2﹣16m+16)2=(m+2)2,
化简得,3m2﹣10m+8=0,
解得m1=![]() ,m2=2(不合题意,舍去),
,m2=2(不合题意,舍去),
∴m=![]() .
.
综合以上可得,当△BEF为直角三角形时,m=0或m=![]() .
.

【题目】某年级共有150名女生,为了解该校女生实心球成绩(单位:米)和仰卧起坐(单位:个)的情况,从中随机抽取30名女生进行测试,获得了她们的相关成绩,并对数据进行整理、描述和分析,下面给出了部分信息.
![]() .实心球成绩的频数分布表如下:
.实心球成绩的频数分布表如下:
分组 | 6.2≤ | 6.6≤ | 7.0≤ | 7.4≤ | 7.8≤ | 8.2≤ |
频数 | 2 |
| 10 | 6 | 2 | 1 |
![]() .实心球成绩在7.0≤
.实心球成绩在7.0≤![]() <7.4.这组的是:
<7.4.这组的是:
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
![]() .一分钟仰卧起坐成绩如图所示:
.一分钟仰卧起坐成绩如图所示:

根据以上信息,回答下列问题:
(1)①表中m的值为 ;
②抽取学生一分钟仰卧起坐成绩的中位数为 个;
(2)若实心球成绩达到7.2米及以上,成绩记为优秀,请估计全年级女生成绩达到优秀的人数.
(3)该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有2名女生的一分钟仰卧起坐成绩未抄录完整,当老师说这8名女生恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.