题目内容
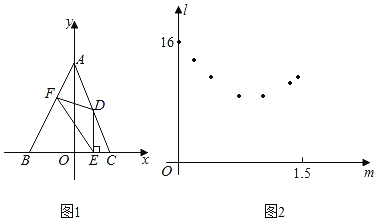
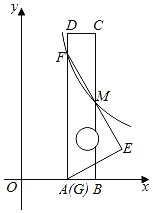
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=![]() (x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=
(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=![]() ,则k=_____.
,则k=_____.
【答案】![]()
【解析】
通过作辅助线,构造直角三角形,求出MN,FN,进而求出AN、MB,表示出点F、点M的坐标,利用反比例函数k的意义,确定点F的坐标,进而确定k的值即可.
解:过点M作MN⊥AD,垂足为N,则MN=AD=3,
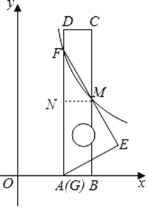
在Rt△FMN中,∠MFN=30°,
∴FN=![]() MN=3
MN=3![]() ,
,
∴AN=MB=8![]() ﹣3
﹣3![]() =5
=5![]() ,
,
设OA=x,则OB=x+3,
∴F(x,8![]() ),M(x+3,5
),M(x+3,5![]() ),
),
∴8![]() x=(x+3)×5
x=(x+3)×5![]() ,
,
解得,x=5,
∴F(5,8![]() ),
),
∴k=5×8![]() =40
=40![]() .
.
故答案为:40![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
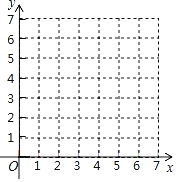
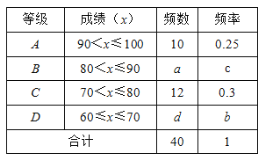
【题目】经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表.
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 6 | 2.9 | 2 | 1.5 | 1.2 | 1 |
(1)请画出相应函数的图象,并求出函数表达式.
(2)点A(x1,y1),B(x2,y2)在此函数图象上.若x1<x2,则y1,y2有怎样的大小关系?请说明理由.