题目内容
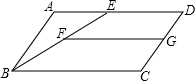
如图,在等腰梯形ABCD中,AD∥BC,BC=10,AD=2,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于______.


过D作DH⊥BC于H,
有三种情况:

如图所示:①当AE=BE时,
∵四边形ABCD是等腰梯形,
∴BE=CH=
(BC-AD)=4,
由勾股定理得:AB=4
,
∴CE=BC-BE=6,
∵∠B=∠BAE=45°,
∴∠AEB=90°,
∴∠FEC=180°-90°-45°=45°=∠C,
∴∠EFC=180°-45°-45°=90°,
∴由勾股定理得:CF=EF=3
,
②当AB=AE=4
时,
由勾股定理求得:BE=8,
∴CE=BC-BE=2,
同法可求出∠FEC=90°,∠EFC=45°=∠C,
由勾股定理得:CF=
=2
,
③

如图当AB=BE=4
时,
∠AEB=∠BAE=
(180°-∠B)=67.5°,
∴∠FEC=180°-67.5°-45°=67.5°,
∵∠C=45°,
∴∠CFE=180°-∠C-∠FEC=67.5°=∠FEC,
∴CF=CE=BC-BE=10-4
,
故答案为:3
或2
或10-4
.
有三种情况:

如图所示:①当AE=BE时,
∵四边形ABCD是等腰梯形,
∴BE=CH=
| 1 |
| 2 |
由勾股定理得:AB=4
| 2 |
∴CE=BC-BE=6,
∵∠B=∠BAE=45°,
∴∠AEB=90°,
∴∠FEC=180°-90°-45°=45°=∠C,
∴∠EFC=180°-45°-45°=90°,
∴由勾股定理得:CF=EF=3
| 2 |
②当AB=AE=4
| 2 |
由勾股定理求得:BE=8,
∴CE=BC-BE=2,
同法可求出∠FEC=90°,∠EFC=45°=∠C,
由勾股定理得:CF=
| EF2+CE2 |
| 2 |
③

如图当AB=BE=4
| 2 |
∠AEB=∠BAE=
| 1 |
| 2 |
∴∠FEC=180°-67.5°-45°=67.5°,
∵∠C=45°,
∴∠CFE=180°-∠C-∠FEC=67.5°=∠FEC,
∴CF=CE=BC-BE=10-4
| 2 |
故答案为:3
| 2 |
| 2 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.