Question

【题目】如图，在等腰梯形ABCD中，AD//BC,AD=2，AB=5，BC=10，点E是边BC上的一个动点（不与B,C重合），作∠AEF=∠AEB,使边EF交边CD于点F,(不与C，D重合），线段BE=______________时，△ABE与△CEF相似。

Answer 1

【答案】或8

【解析】

分类讨论，当∠AEB=∠FEC时，根据正切函数，可得ME的长，根据线段的和差，可得答案，当∠AEB=∠EFC时，根据等腰三角形的性质，可得BM与ME的关系，根据线段的和差，可得答案；

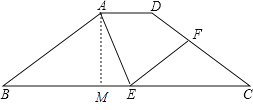
解：如图：过A作AM⊥BC，过D作DN⊥BC，
∵等腰梯形ABCD，AM⊥BC，DN⊥BC，AD=2，BC=10，
∴BM=CN=4，BN=6，
又AB=5，
∴，
∴DN=AM=3

△ABE与△CEF相似有两种情况，

（1）当∠AEB=∠FEC时
∵∠AEF=∠AEB
∴∠AEF=∠AEB=∠FEC=60°
由（1）知：AM=3，BM=4
∴，
∴，

（2）当∠AEB=∠EFC时，
∵∠AEF=∠AEB，
∴∠AEF=∠EFC，
∴AE∥DC，
∴∠AEB=∠C=∠B，
∴△ABE是等腰三角形，

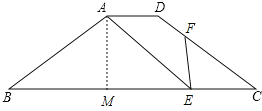
如图，过A 作AM⊥BC，
∴BM=ME（等腰三角形三线合一性质）．
∵BM=4，
∴BE=2BM=8，
综上，当△ABE∽△CEF时，BE的长为或8；