Question

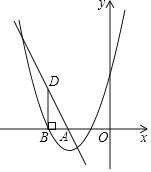
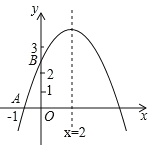
【题目】如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：

①abc＜0；②9a+3b+c＞0；③若点M（，y1），点N（，y2）是函数图象上的两点，则y1＞y2；④﹣＜a＜﹣；⑤c-3a＞0．

其中正确结论有（　　）

A.1个B.2个C.3个D.4个

Answer 1

【答案】D

【解析】

①根据二次函数图像与系数的关系可知：开口向下，a＜0；对称轴在y轴右侧，根据“左同右异”可知a、b异号，则b＞0；图像与y轴交于正半轴，则c＞0，据此可判断；

②根据抛物线对称性，可得图像与x轴的另一交点为（5,0），由图像可知当x=3时，y＞0，可判断；

③找出N（，y2）关于对称轴的对称点，再用二次函数的增减性判断大小；

④根据对称轴x=2，可得，将（-1,0）代入函数解析式可得，最后B在（0，2）与（0，3）之间可判断a的取值范围.

⑤由，可得.

①抛物线开口向上，∴

对称轴，∴（左同右异）

抛物线与y轴交于正半轴，∴

∴abc＜0，故①正确；

②∵图象与x轴交于点A（﹣1，0），对称轴为直线x=2，

∴图像与x轴的另一交点为（5,0），当x=3时，y＞0，

∴9a+3b+c＞0，故②正确；

③N（，y2）关于对称轴x=2的对称点为（，y2），

，根据抛物线图像可知在对称轴左侧，y随x的增大而增大，

∴y1＜y2，故③错误；

④对称轴，∴，

将（-1,0）代入二次函数可得，∴，，

∵，∴，解得﹣＜a＜﹣，故④正确；

⑤由④中可得，故⑤正确.

所以选D.