题目内容
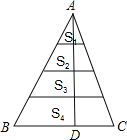
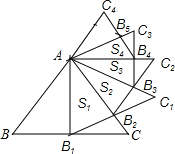
【题目】如图，等边三角形ABC的边长为2，以BC边上的高AB1为边作等边三角形AB1C1，△ABC与△AB1C1公共部分的面积记为S1，再以等边三角形AB1C1边B1C1上的高AB2为边作等边三角形AB2C2，△AB1C1与△AB2C2公共部分的面积记为S2……以此类推，那么S3_____．（用含n的式子表示）
【答案】
【解析】
由AB1为边长为2的等边三角形ABC的高，利用三线合一得到B1为BC的中点，求出BB1的长，利用勾股定理求出AB1的长，进而求出S1，同理求出S2，依此类推，得到Sn．
解：∵等边三角形ABC的边长为2，AB1⊥BC，
∴BB1＝1，AB＝2，
根据勾股定理得：AB1＝
∴S1＝
×
×
＝
∵等边三角形AB1C1的边长为，AB2⊥B1C1，
∴B1B2＝
，AB1＝，
根据勾股定理得：AB2＝
，
∴S2＝
＝
，
依此类推，Sn＝
，
故答案为．
练习册系列答案
相关题目
