Question

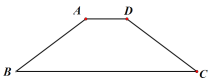
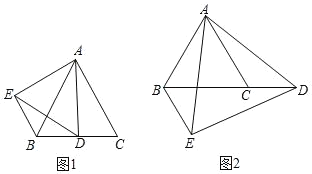
【题目】如图，在△ABC中，AB=AC，∠C=60°，点D是射线BC上的一个动点（点D不与点B、C重合），△ADE是以AD为一边的等边三角形．

（1）如图①，当点D在线段BC上时，求证：△AEB≌△ADC；

（2）如图①，探究BE和AC的位置关系，并说明理由．

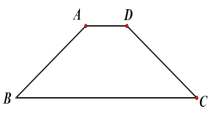
（3）如图②，当点D在BC的延长线上时，（2）中结论还成立吗？说明理由．

Answer 1

【答案】（1）证明见解析；（2）BE∥AC；理由见解析；（3）成立；理由见解析.

【解析】

(1)可求出∠EAB=∠DAC，随即利用SAS即可证明全等.

(2) 根据△AEB≌△ADC可得∠ABE=∠C=∠BAC =60°，再利用∠ABE=∠BAC可求平行.

(3) △AEB≌△ADC依旧成立，可证明∠AEB=∠EAC，随即可得平行.

（1）证明：∵AB=AC，∠C=60°，

∴△ABC是等边三角形，

∴∠BAC=60°，

∵△ADE是等边三角形，

∴AE=AD，∠EAD=60°，

∴∠EAB=∠DAC，

在△AEB和△ADC中，

，

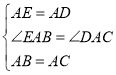∴△AEB≌△ADC（SAS）；

（2）解：BE∥AC，

理由如下：∵△AEB≌△ADC，

∴∠ABE=∠C=60°，

∴∠ABE=∠BAC，

∴BE∥AC；

（3）解：成立，

理由如下：由（1）的方法可以证明△AEB≌△ADC，

∴∠AEB=∠ADC，

∵∠ADC+∠CAD=∠ACB=60°，∠EAC+∠CAD=∠EAD=60°，

∴∠ADC=∠EAC，

∴∠AEB=∠EAC，

∴BE∥AC．