Question

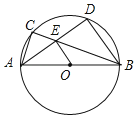
【题目】如图，⊙I是△ABC的内切圆，切点分别是D、E、F．

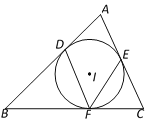
（1）若∠B＝50°，∠C＝70°，则∠DFE的度数为 ；

（2）若∠DFE＝50°，求∠A的度数．

Answer 1

【答案】（1）60°；（2）∠A＝80°

【解析】

（1）连接DI和EI，根据三角形的内角和定理求得∠A=60°，再根据切线的性质以及四边形的内角和定理，得∠DOE=120°，再根据圆周角定理得∠DFE=60°；

（2）根据圆周角定理得∠DOE=100°，再根据切线的性质以及四边形的内角和定理，得∠A＝80°.

（1） 连接ID、IE

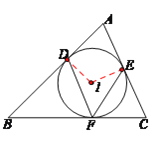
由题可知：∠A=180°-∠B -∠C=180°-50° -70°= 60°

∵AD、AE分别切⊙I 于D、E

∴DI⊥AB，IE⊥AC

∴∠ADI＝∠AEI＝90°

∴∠DIE＝120°

∴∠DFE＝60°

（2）∵∠DFE＝50°

∴∠DIE＝100°

∵AD、AE分别切⊙I 于D、E

∴DI⊥AD，IE⊥AE

∴∠ADI＝∠AEI＝90°

∴∠A＝80°