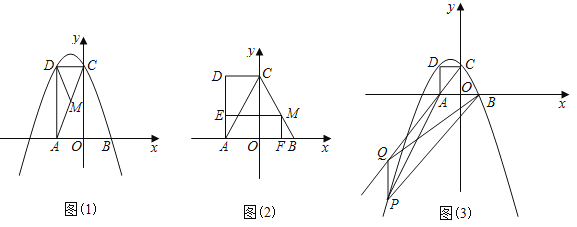��Ŀ����
����Ŀ���ڡ�ABC�У�AB��AC����A��60�㣬��D���߶�BC���е㣬��EDF��120�㣬DE���߶�AB�ཻ�ڵ�E��DF���߶�AC����AC���ӳ��ߣ��ཻ�ڵ�F��
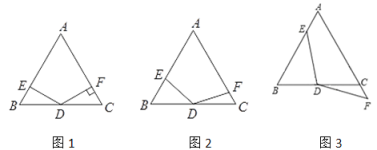
��1����ͼ1����DF��AC������ΪF��֤����DE��DF
��2����ͼ2������EDF�Ƶ�D˳ʱ����תһ���ĽǶȣ�DF�����߶�AC�ཻ�ڵ�F��DE��DF��Ȼ������˵�����ɣ�
��3����ͼ3������EDF�����Ƶ�D˳ʱ����תһ���ĽǶȣ�ʹDF���߶�AC���ӳ����ཻ�ڵ�F��DE��DF��Ȼ������˵�����ɣ�
���𰸡���1������������2��������Ȼ����.��DE��DF������������3����Ȼ������DE��DF��������
��������
��1�����������ȫ�������ε��������ж�����ϵȱ�����������֤����BED�ա�CFD��ASA��������֤��DE��DF��
��2������������ȡAC�е�G,����DG,�̶���ȫ�������ε��������ж�����ϵȱ�����������֤����EDG�ա�FDC��ASA��������֤��DE��DF��
��3�����������D��DN��AC��N,DM��AB��M, �̶���ȫ�������ε��������ж�����ϵȱ�����������֤����DME�ա�DNF��ASA��������֤��DE��DF��
�⣺��1����AB=AC����A=60����
���ABC�ǵȱ�������,����B=��C=60��,
��D��BC���е�,
��BD=CD,
�ߡ�EDF=120����DF��AC��
���FDC=30��,
���EDB=30����
���BED�ա�CFD��ASA��,
��DE=DF.
��2��ȡAC�е�G,����DG,����ͼ,
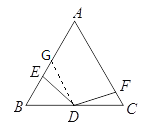
��DΪBC���е�,
��DG=![]() AC=BD=CD,
AC=BD=CD,
���BDG�ǵȱ�������,
���GDE+��EDB=60��,
�ߡ�EDF=120��,
���FDC+��EDB=60��,
���EDG=��FDC,
���EDG�ա�FDC��ASA��,
��DE=DF��
��������Ȼ����.
��3������ͼ,����D��DN��AC��N,DM��AB��M,

���DME=��DNF=90��,
�ɣ�1����֪��B=��C=60��,
���NDC=��BDM=30��,DM=DN,
���MDN=120��,����NDF=��MDE,
���DME�ա�DNF��ASA��,
��DE=DF,
����Ȼ����.

 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�