题目内容
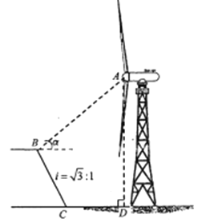
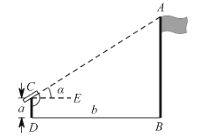
【题目】如图,小明想要测量学校操场上旗杆![]() 的高度,他作了如下操作:(1)在点
的高度,他作了如下操作:(1)在点![]() 处放置测角仪,测得旗杆顶的仰角
处放置测角仪,测得旗杆顶的仰角![]() ;(2)量得测角仪的高度
;(2)量得测角仪的高度![]() ;(3)量得测角仪到旗杆的水平距离
;(3)量得测角仪到旗杆的水平距离![]() .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
延长CE交AB于F,得四边形CDBF为矩形,故CF=DB=b,FB=CD=a,在直角三角形ACF中,利用CF的长和已知的角的度数,利用正切函数可求得AF的长,从而可求出旗杆AB的长.
延长CE交AB于F,如图,
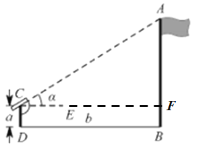
根据题意得,四边形CDBF为矩形,
∴CF=DB=b,FB=CD=a,
在Rt△ACF中,∠ACF=α,CF=b,
tan∠ACF=![]()
∴AF=![]() ,
,
AB=AF+BF=![]() ,
,
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
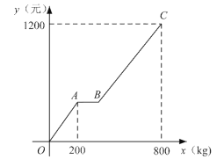
【题目】某商店代理销售一种水果,六月份的销售利润![]() (元)与销售量
(元)与销售量![]() 之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
日期 | 销售记录 |
6月1日 | 库存 |
6月9日 | 从6月1日至今,一共售出 |
6月10、11日 | 这两天以成本价促销,之后售价恢复到10元/ |
6月12日 | 补充进货 |
6月30日 |
|
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图像中线段![]() 所在直线对应的函数表达式.
所在直线对应的函数表达式.