��Ŀ����
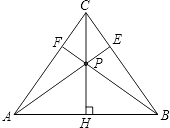
����Ŀ����ͼ���ڵ�����ABC�У�CH�ǵױ��ϵĸ��ߣ���P���߶�CH�ϲ���˵��غϵ�����һ�㣬����AP��BC�ڵ�E������BP��AC�ڵ�F�� 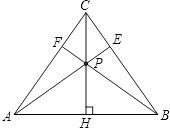
��1��֤������CAE=��CBF��
��2��֤����AE=BF��
��3�����߶�AE��BF��ABΪ�߹���һ���µ�������ABG����E���F�غ��ڵ�G�����ǡ�ABC�͡�ABG������ֱ�ΪS��ABC��S��ABG �� ������ڵ�P����ʹ��S��ABC=S��ABG �� ���ACB��ȡֵ��Χ��
���𰸡�
��1��֤�����ߡ�ABC�ǵ��������Σ�CH�ǵױ��ϵĸ��ߣ�
��AC=BC����ACP=��BCP��
�֡�CP=CP��
���ACP�ա�BCP��
���CAP=��CBP������CAE=��CBF��
��2��֤�������ڡ�ACE���BCF�У�
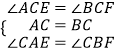 ��
��
���ACE�ա�BCF��ASA����
��AE=BF��
��3���⣺���ɣ�2��֪��ABG����ABΪ�ױߵĵ��������Σ�
��S��ABC=S��ABG��
��AE=AC��
�ٵ���ACBΪֱ�ǻ�۽�ʱ���ڡ�ACE�У����۵�P��CH�δ�������AE��AC�����Խ��۲�������
�ڵ���ACBΪ���ʱ����CAH=90�㩁 ![]() ��ACB������CAE����CAH��ҪʹAE=AC��ֻ��ʹ��ACB=��CEA��
��ACB������CAE����CAH��ҪʹAE=AC��ֻ��ʹ��ACB=��CEA��
��ʱ����CAE=180�㩁2��ACB��
ֻ��180�㩁2��ACB��90�㩁 ![]() ��ACB��
��ACB��
��ã�60�㣼��ACB��90�㣮
����������1��֤�á�ACP�ա�BCP���ɣ���2�����ϣ�1���Ľ��ۣ�֤�á�ACE�ա�BCF���ɣ���3��������ڵ�P����ʹ��S��ABC=S��ABG �� �ɣ�2���õ���AE=BF������������ABGҲΪ���������Σ����ݵױ߶�ΪAB�������ȣ��õ�����ȣ�����AC=AE����������ACEΪ���������Σ���ǡ�ACBΪ��ǣ����ɵõ���ACB��ȡֵ��Χ��
�����㾫�������ڱ��⿼��ĵ��������ε����ʣ���Ҫ�˽���������ε���������ȣ���ƣ��ȱ߶ԵȽǣ����ܵó���ȷ�𰸣�

 ������ϵ�д�
������ϵ�д�