题目内容
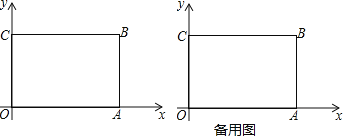
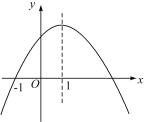
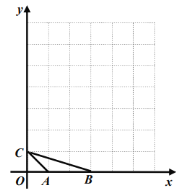
【题目】如图,已知A(-1,0),一次函数![]() 的图像交坐标轴于点B、C,二次函数
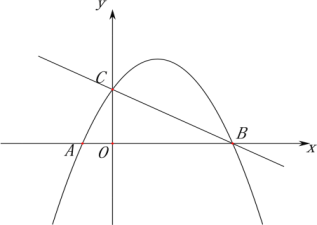
的图像交坐标轴于点B、C,二次函数![]() 的图像经过点A、C、B.点Q是二次函数图像上一动点。
的图像经过点A、C、B.点Q是二次函数图像上一动点。
(1)当![]() 时,求点Q的坐标;
时,求点Q的坐标;
(2)过点Q作直线![]() //BC,当直线
//BC,当直线![]() 与二次函数的图像有且只有一个公共点时,求出此时直线
与二次函数的图像有且只有一个公共点时,求出此时直线![]() 对应的一次函数的表达式并求出此时直线
对应的一次函数的表达式并求出此时直线![]() 与直线BC之间的距离。
与直线BC之间的距离。
【答案】(1)Q(0,2)或(3,2)或Q(![]() ,-2)或Q(
,-2)或Q(![]() ,-2);(2)一次函数
,-2);(2)一次函数![]() ,此时直线
,此时直线![]() 与直线BC之间的距离为
与直线BC之间的距离为![]()
【解析】
(1)根据![]() 可求得Q点的纵坐标,将Q点的纵坐标代入求得的二次函数解析式中求出Q点的横坐标,即可求得Q点的坐标;
可求得Q点的纵坐标,将Q点的纵坐标代入求得的二次函数解析式中求出Q点的横坐标,即可求得Q点的坐标;
(2)根据两直线平行可得直线l的一次项系数,因为直线与抛物线只有一个交点,所以联立它们所形成的方程组有两个相同的解可求得直线l的常数项,即可得到它的解析式.利用等面积法可求得原点距离两直线的距离,距离差即为直线![]() 与直线BC之间的距离.
与直线BC之间的距离.
解:(1)对于一次函数![]() ,
,
当x=0时,y=2,所以C(0,2),当y=0时,x=4,所以B(4,0).
∴![]() .
.
∴![]() 则
则![]() ,
,
将A、B带入二次函数解析式得![]() ,解得
,解得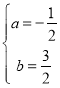 ,
,
∴二次函数解析式为:![]() ,
,
当y=2时,![]() ,解得
,解得![]() ,
,
所以![]() ,
,
当y=-2时,![]() ,解得
,解得![]() ,
,
所以![]() ,
,
故Q(0,2)或(3,2)或Q(![]() ,-2)或Q(
,-2)或Q(![]() ,-2).
,-2).
(2)根据题意设一次函数![]() ,
,
∵直线![]() 与二次函数的图像有且只有一个公共点
与二次函数的图像有且只有一个公共点
∴![]() 只有一个解,
只有一个解,
整理得![]() ,
,
∴![]() ,解得b=4,
,解得b=4,
∴一次函数![]()
如下图,直线l与坐标轴分别相交于D,E,过O作直线BC的垂线与BC和DE相交于F和G,
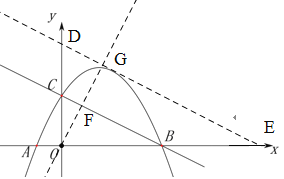
对于一次函数![]() ,当x=0时,y=4,故D(0,4),当y=0时,x=8,故E(8,0).
,当x=0时,y=4,故D(0,4),当y=0时,x=8,故E(8,0).
∴![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() .
.
∴此时直线![]() 与直线BC之间的距离为
与直线BC之间的距离为![]() .
.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目